Question

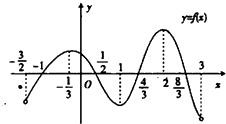函数y=f（x）在定义域(-

3

2

，3)内可导，其图象如图，记y=f（x）的导函数为y=f^/（x），则不等式f^/（x）＜0的解集为

 

．

Answer 1

分析：当函数为单调递减时f^/（x）＜0，所以本题只要找出函数的递减区间即可．

解答：解：如图，函数y=f（x）在区间[-

1

3

，1]和区间[2，3），
∴在区间[-

1

3

，1]和区间[2，3），y=f^/（x）＜0，
∴f′（x）＜0的解集为[-

1

3

，1]∪[2，3)．
故答案为：[-

1

3

，1]∪[2，3)．

点评：本题主要考查了利用导数研究函数的单调性．一定要记住导数与函数单调性的关系．