题目内容
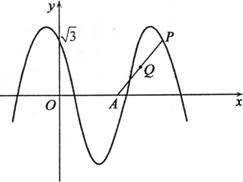
 如图,函数y=2cos(ωx+θ)(x∈R,0≤θ≤
如图,函数y=2cos(ωx+θ)(x∈R,0≤θ≤| π |
| 2 |
| 3 |
(1)求θ和ω的值;
(2)已知点A(
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
分析:(1)根据(0,
)以及θ的范围,求θ,利用导数和斜率的关系求ω的值;
(2)利用点A(
,0),点Q(x0,y0)求出P,点P是该函数图象上一点,代入表达式,利用y0=
,x0∈[
,π],求x0的值.
| 3 |
(2)利用点A(
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
解答:解:(1)将x=0,y=
代入函数y=2cos(ωx+θ)得cosθ=
,
因为0≤θ≤
,所以θ=
.
又因为y'=-2ωsin(ωx+θ),y'|x=0=-2,θ=
,所以ω=2,
因此y=2cos(2x+
).
(2)因为点A(
,0),Q(x0,y0)是PA的中点,y0=
,
所以点P的坐标为(2x0-
,
).
又因为点P在y=2cos(2x+
)的图象上,所以cos(4x0-
)=
.
因为
≤x0≤π,所以
≤4x0-
≤
,
从而得4x0-
=
或4x0-
=
.
即x0=
或x0=
.
| 3 |
| ||
| 2 |
因为0≤θ≤
| π |
| 2 |
| π |
| 6 |
又因为y'=-2ωsin(ωx+θ),y'|x=0=-2,θ=
| π |
| 6 |
因此y=2cos(2x+
| π |
| 6 |
(2)因为点A(
| π |
| 2 |
| ||
| 2 |
所以点P的坐标为(2x0-
| π |
| 2 |
| 3 |
又因为点P在y=2cos(2x+
| π |
| 6 |
| 5π |
| 6 |
| ||
| 2 |
因为
| π |
| 2 |
| 7π |
| 6 |
| 5π |
| 6 |
| 19π |
| 6 |
从而得4x0-
| 5π |
| 6 |
| 11π |
| 6 |
| 5π |
| 6 |
| 13π |
| 6 |
即x0=
| 2π |
| 3 |
| 3π |
| 4 |
点评:本题考查y=Asin(ωx+φ)中参数的物理意义,导数的运算,考查分析问题解决问题的能力,是中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
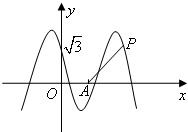
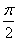 ) 的图象与y轴交于点(0,
) 的图象与y轴交于点(0,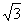 ),且在该点处切线的斜率为-2,
),且在该点处切线的斜率为-2, ,0),点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,0),点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=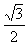 ,x0∈[
,x0∈[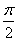 ,π]时,求x0的值。
,π]时,求x0的值。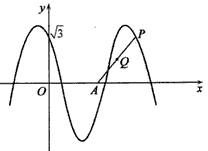
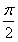 ) 的图象与y轴交于点(0,
) 的图象与y轴交于点(0,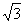 ),且该函数的最小正周期为π,
),且该函数的最小正周期为π,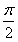 ,0),点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,0),点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=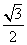 ,x0∈[
,x0∈[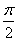 ,π]时,求x0的值。
,π]时,求x0的值。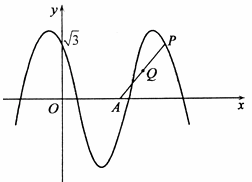
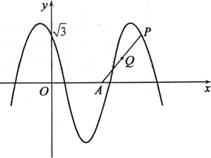 如图,函数y=2cos(ωx+θ) (x∈R,0≤θ≤
如图,函数y=2cos(ωx+θ) (x∈R,0≤θ≤