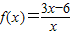Question

求函数y=4^x-2^x+1 x∈[-3，2]的最大值与最小值．

Answer 1

分析：令2^x=t，由-3≤x≤2，可得

1

8

≤t≤4，y=t²-t+1，t∈[

1

8

，4]．再利用二次函数的性质求得y的最值．

解答：解：y=（2^x）²-2^x+1，令2^x=t，
∵-3≤x≤2，∴

1

8

≤2x≤4，
∴y=t²-t+1，t∈[

1

8

，4]．
由于函数 y=(t-

1

2

)2+

3

4

的对称轴为 t=

1

2

，
∴当t=

1

2

时，ymin=

3

4

，当t=4时，y_max=16-4+1=13．

点评：本题主要考查复合函数的单调性，二次函数的性质的应用，属于中档题．