题目内容
 如图,已知椭圆G:
如图,已知椭圆G: 的右准线l1:x=4与x轴交与点M,点A,F2分别是的右顶点和右焦点,且MA=2AF2.过点A作斜率为-1的直线l2交椭圆于另一点B,以AB为底边作等腰三角形ABC,点C恰好在直线l1上.
的右准线l1:x=4与x轴交与点M,点A,F2分别是的右顶点和右焦点,且MA=2AF2.过点A作斜率为-1的直线l2交椭圆于另一点B,以AB为底边作等腰三角形ABC,点C恰好在直线l1上.
(1)求椭圆G的方程;
(2)求△ABC的面积.
解:(1)由MA=2AF2,得椭圆的离心率为 ,即a=2c.
,即a=2c.
又椭圆的右准线l1:x=4,所以 ,所以a=2,c=1.
,所以a=2,c=1.
所以求椭圆G的方程为 .
.
(2)∵过点A作斜率为-1的直线l2,
∴直线l2的方程为y=-x+2,
解方程组 ,得
,得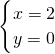 或
或 ,即
,即
∵A(2,0),∴ ,
,
所以AB中点 .
.
AB的垂直平分线方程为 ,即
,即 ,
,
令x=4,得 ,即
,即 .
.
所以 ,
, ,
,
所以△ABC的面积 .
.
分析:(1)由MA=2AF2,得椭圆的离心率为 ,从而a=2c,又椭圆的右准线l1:x=4,所以
,从而a=2c,又椭圆的右准线l1:x=4,所以 ,所以a=2,c=1,从而可求椭圆G的方程;
,所以a=2,c=1,从而可求椭圆G的方程;
(2)直线l2的方程为y=-x+2,解方程组 ,可得
,可得 ,所以AB中点
,所以AB中点 ,从而可得AB的垂直平分线方程为
,从而可得AB的垂直平分线方程为 ,由此可求
,由此可求 ,所以
,所以 ,
, ,故可求△ABC的面积.
,故可求△ABC的面积.
点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形的面积,综合性强.
 ,即a=2c.
,即a=2c.又椭圆的右准线l1:x=4,所以
 ,所以a=2,c=1.
,所以a=2,c=1.所以求椭圆G的方程为
 .
.(2)∵过点A作斜率为-1的直线l2,
∴直线l2的方程为y=-x+2,
解方程组
 ,得
,得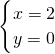 或
或 ,即
,即∵A(2,0),∴
 ,
,所以AB中点
 .
.AB的垂直平分线方程为
 ,即
,即 ,
,令x=4,得
 ,即
,即 .
.所以
 ,
, ,
,所以△ABC的面积
 .
.分析:(1)由MA=2AF2,得椭圆的离心率为
 ,从而a=2c,又椭圆的右准线l1:x=4,所以
,从而a=2c,又椭圆的右准线l1:x=4,所以 ,所以a=2,c=1,从而可求椭圆G的方程;
,所以a=2,c=1,从而可求椭圆G的方程;(2)直线l2的方程为y=-x+2,解方程组
 ,可得
,可得 ,所以AB中点
,所以AB中点 ,从而可得AB的垂直平分线方程为
,从而可得AB的垂直平分线方程为 ,由此可求
,由此可求 ,所以
,所以 ,
, ,故可求△ABC的面积.
,故可求△ABC的面积.点评:本题以椭圆的性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形的面积,综合性强.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
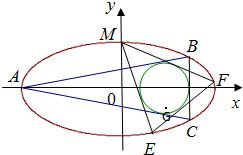 如图,已知圆G:(x-2)2+y2=r2是椭圆
如图,已知圆G:(x-2)2+y2=r2是椭圆 如图,已知椭圆G:
如图,已知椭圆G: (2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0
(2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0 的右准线l1:x=4与x轴交与点M,点A,F2分别是的右顶点和右焦点,且MA=2AF2.过点A作斜率为-1的直线l2交椭圆于另一点B,以AB为底边作等腰三角形ABC,点C恰好在直线l1上.
的右准线l1:x=4与x轴交与点M,点A,F2分别是的右顶点和右焦点,且MA=2AF2.过点A作斜率为-1的直线l2交椭圆于另一点B,以AB为底边作等腰三角形ABC,点C恰好在直线l1上.