题目内容
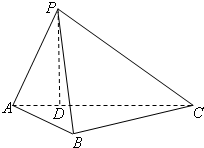 (2012•广州一模)如图所示,在三棱锥P-ABC中,AB=BC=
(2012•广州一模)如图所示,在三棱锥P-ABC中,AB=BC=| 6 |
(1)求三棱锥P-ABC的体积;
(2)证明△PBC为直角三角形.
分析:(1)利用面面垂直的性质,证明PD⊥平面ABC,再计算△ABC的面积,即可求三棱锥P-ABC的体积;
(2)证法1:计算出BC,PB,PC,利用BC2+PB2=PC2,可得结论;
证法2:利用线面垂直的判定证明BC⊥平面PBD,从而BC⊥PB.
(2)证法1:计算出BC,PB,PC,利用BC2+PB2=PC2,可得结论;
证法2:利用线面垂直的判定证明BC⊥平面PBD,从而BC⊥PB.
解答: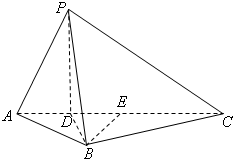 (1)解:因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,所以PD⊥平面ABC.…(2分)
(1)解:因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,所以PD⊥平面ABC.…(2分)
记AC边上的中点为E,
在△ABC中,因为AB=BC,所以BE⊥AC.
因为AB=BC=
,AC=4,
所以BE=
=
=
.…(4分)
所以△ABC的面积S△ABC=
×AC×BE=2
.…(5分)
因为PD=2,所以三棱锥P-ABC的体积VP-ABC=
×S△ABC×PD=
×2
×2=
.…(7分)
(2)证法1:因为PD⊥AC,所以△PCD为直角三角形.
因为PD=2,CD=3,所以PC=
=
=
.…(9分)
连接BD,在Rt△BDE中,因为∠BED=90°,BE=
,DE=1,
所以BD=
=
=
.…(10分)
由(1)知PD⊥平面ABC,又BD?平面ABC,所以PD⊥BD.
在Rt△PBD中,因为∠PDB=90°,PD=2,BD=
,
所以PB=
=
=
.…(12分)
在△PBC中,因为BC=
,PB=
,PC=
,
所以BC2+PB2=PC2.…(13分)
所以△PBC为直角三角形.…(14分)
证法2:连接BD,在Rt△BDE中,因为∠BED=90°,BE=
,DE=1,
所以BD=
=
=
.…(8分)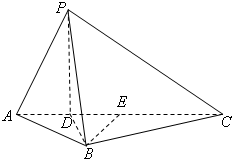
在△BCD中,CD=3,BC=
,BD=
,
所以BC2+BD2=CD2,所以BC⊥BD.…(10分)
由(1)知PD⊥平面ABC,
因为BC?平面ABC,所以BC⊥PD.
因为BD∩PD=D,所以BC⊥平面PBD.…(12分)
因为PB?平面PBD,所以BC⊥PB.
所以△PBC为直角三角形.…(14分)
 (1)解:因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,所以PD⊥平面ABC.…(2分)
(1)解:因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PD?平面PAC,PD⊥AC,所以PD⊥平面ABC.…(2分)记AC边上的中点为E,
在△ABC中,因为AB=BC,所以BE⊥AC.
因为AB=BC=
| 6 |
所以BE=
| BC2-CE2 |
(
|
| 2 |
所以△ABC的面积S△ABC=
| 1 |
| 2 |
| 2 |
因为PD=2,所以三棱锥P-ABC的体积VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
4
| ||
| 3 |
(2)证法1:因为PD⊥AC,所以△PCD为直角三角形.
因为PD=2,CD=3,所以PC=
| PD2+CD2 |
| 22+32 |
| 13 |
连接BD,在Rt△BDE中,因为∠BED=90°,BE=
| 2 |
所以BD=
| BE2+DE2 |
(
|
| 3 |
由(1)知PD⊥平面ABC,又BD?平面ABC,所以PD⊥BD.
在Rt△PBD中,因为∠PDB=90°,PD=2,BD=
| 3 |
所以PB=
| PD2+BD2 |
22+(
|
| 7 |
在△PBC中,因为BC=
| 6 |
| 7 |
| 13 |
所以BC2+PB2=PC2.…(13分)
所以△PBC为直角三角形.…(14分)
证法2:连接BD,在Rt△BDE中,因为∠BED=90°,BE=
| 2 |
所以BD=
| BE2+DE2 |
(
|
| 3 |

在△BCD中,CD=3,BC=
| 6 |
| 3 |
所以BC2+BD2=CD2,所以BC⊥BD.…(10分)
由(1)知PD⊥平面ABC,
因为BC?平面ABC,所以BC⊥PD.
因为BD∩PD=D,所以BC⊥平面PBD.…(12分)
因为PB?平面PBD,所以BC⊥PB.
所以△PBC为直角三角形.…(14分)
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 (2012•广州一模)如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以a表示.已知甲、乙两个小组的数学成绩的平均分相同.
(2012•广州一模)如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以a表示.已知甲、乙两个小组的数学成绩的平均分相同.