题目内容
【题目】如图，△ABC内接于直径为BC的圆O，过点A作圆O的切线交CB的延长线于点P，∠BAC的平分线分别交BC和圆O于点D、E，若PA=2PB=10．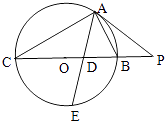 
（1）求证：AC=2AB；
（2）求ADDE的值．
【答案】
（1）解：∵PA是圆O的切线∴∠PAB=∠ACB又∠P是公共角
∴△ABP∽△CAP
∴ 
∴AC=2AB
（2）解：由切割线定理得：PA2=PBPC∴PC=20
又PB=5∴BC=15
又∵AD是∠BAC的平分线∴ 
∴CD=2DB∴CD=10，DB=5…（8分）
又由相交弦定理得：ADDE=CDDB=50
【解析】（1）通过证明△ABP∽△CAP，然后证明AC=2AB；（2）利用切割线定理以及相交弦定理直接求ADDE的值．
练习册系列答案
备战中考寒假系列答案
相关题目
