题目内容
P是双曲线x2- =1右支上一点,F1、F2分别是左、右焦点,I是三角形PF1F2的内心(三条内角平分线交点),若
=1右支上一点,F1、F2分别是左、右焦点,I是三角形PF1F2的内心(三条内角平分线交点),若 =2
=2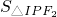 +(1+
+(1+ )
)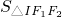 ,则实数λ的值为________.
,则实数λ的值为________.
2
分析:利用三角形的面积公式与双曲线的定义,可求得λ= ,从而可求得答案.
,从而可求得答案.
解答:依题意,设双曲线x2- =1的焦距为2c,实轴长为2a,则c=2,a=1.
=1的焦距为2c,实轴长为2a,则c=2,a=1.
∵I是三角形PF1F2的内心,设三角形PF1F2的内切圆的半径为r,
则: =
= (|F1F2|+|PF1|+|PF2|)r,
(|F1F2|+|PF1|+|PF2|)r,
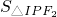 =
= |PF2|r,
|PF2|r,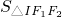 =
= |F1F2|r,
|F1F2|r,
∵ =2
=2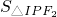 +(1+
+(1+ )
)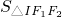 ,
,
又 =
=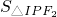 +
+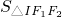 +
+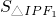 ,
,
∴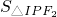 +
+
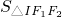 =
=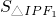 ,
,
即 |PF2|r|+
|PF2|r|+ ×
× |F1F2|r=
|F1F2|r= |PF1|r,
|PF1|r,
∴|PF2|+ |F1F2|=|PF1|,又P是双曲线x2-
|F1F2|=|PF1|,又P是双曲线x2- =1右支上一点,
=1右支上一点,
∴ =
=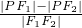 =
= =
= =
= ,
,
∴λ=2.
故答案为:2.
点评:本题考查三角形的面积公式与双曲线的定义及性质(离心率)的应用,求得λ= 是关键,考查转化与综合运用的能力,属于中档题.
是关键,考查转化与综合运用的能力,属于中档题.
分析:利用三角形的面积公式与双曲线的定义,可求得λ=
 ,从而可求得答案.
,从而可求得答案.解答:依题意,设双曲线x2-
 =1的焦距为2c,实轴长为2a,则c=2,a=1.
=1的焦距为2c,实轴长为2a,则c=2,a=1.∵I是三角形PF1F2的内心,设三角形PF1F2的内切圆的半径为r,
则:
 =
= (|F1F2|+|PF1|+|PF2|)r,
(|F1F2|+|PF1|+|PF2|)r,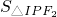 =
= |PF2|r,
|PF2|r,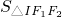 =
= |F1F2|r,
|F1F2|r,∵
 =2
=2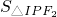 +(1+
+(1+ )
)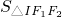 ,
,又
 =
=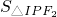 +
+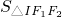 +
+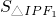 ,
,∴
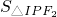 +
+
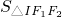 =
=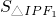 ,
,即
 |PF2|r|+
|PF2|r|+ ×
× |F1F2|r=
|F1F2|r= |PF1|r,
|PF1|r,∴|PF2|+
 |F1F2|=|PF1|,又P是双曲线x2-
|F1F2|=|PF1|,又P是双曲线x2- =1右支上一点,
=1右支上一点,∴
 =
=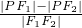 =
= =
= =
= ,
,∴λ=2.
故答案为:2.
点评:本题考查三角形的面积公式与双曲线的定义及性质(离心率)的应用,求得λ=
 是关键,考查转化与综合运用的能力,属于中档题.
是关键,考查转化与综合运用的能力,属于中档题. 
练习册系列答案
相关题目
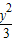 =1上的一点F1、F2分别是双曲线的左、右焦点,若|PF1|=
=1上的一点F1、F2分别是双曲线的左、右焦点,若|PF1|=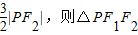 的面积为( )
的面积为( )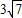
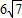
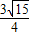
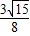
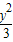 =1右支上一点,F1、F2分别是左、右焦点,I是三角形PF1F2的内心(三条内角平分线交点),若
=1右支上一点,F1、F2分别是左、右焦点,I是三角形PF1F2的内心(三条内角平分线交点),若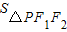 =2
=2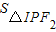 +(1+
+(1+ )
)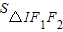 ,则实数λ的值为 .
,则实数λ的值为 .