题目内容
△ABC满足以下条件,求a的值.
(1)b=![]() ,c=1,B=45°;
,c=1,B=45°;
(2)C=45°,B=30°,b=![]() .
.
答案:
解析:
解析:
|
(1)解法一:由余弦定理b2=a2+c2-2accos45°,得a2- 解法二:由正弦定理得sinC= 又c<b,∴C=30°. ∴A=180°-(B+C)=180°-(30°+45°)=105°. ∴a= (2)解:由A+B+C=180°,得A=105°, 由正弦定理得a= 解析:(1)是已知两边及一边的对角,可利用正弦定理,也可利用余弦定理;(2)是已知两角及一边,可用A+B+C=180°求得A,再利用正弦定理求解. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
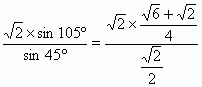 =
=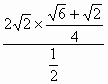 =
=