题目内容
已知三棱锥P-ABC中,PA、PB、PC两两垂直,PA=PB=2PC=2a,且三棱锥外接球的表面积为S=9π,则实数a的值为( )
A. B.2 C. 1 D.
A. B.2 C. 1 D.
C
由题意可知三棱锥是长方体的一个角,长方体的对角线的长,就是外接球的直径,求出直径,然后求出a的值.
解:由题意可知三棱锥是长方体的一个角,
所以长方体的对角线的长,就是外接球的直径,
所以外接球的表面积为S=9π=4πR2,直径为3;
所以由几何体的结构特征可得:9=a2+4a2+4a2=9a2,
所以a=1
故选C.
解:由题意可知三棱锥是长方体的一个角,
所以长方体的对角线的长,就是外接球的直径,
所以外接球的表面积为S=9π=4πR2,直径为3;
所以由几何体的结构特征可得:9=a2+4a2+4a2=9a2,
所以a=1
故选C.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
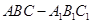 的侧棱长和底面边长均为
的侧棱长和底面边长均为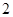 ,且侧棱
,且侧棱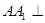 底面
底面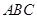 ,
,












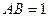 ,若二面角C-AB-C1的大小为600,则点C到平面ABC1的距离为
,若二面角C-AB-C1的大小为600,则点C到平面ABC1的距离为 

 为
为 的中点,求证
的中点,求证 :
: 平面
平面 ;
; 与平面
与平面
 的顶点P在底面
的顶点P在底面 中的投影恰好是
中的投影恰好是 ,其三视图如图所示,则四棱锥
,其三视图如图所示,则四棱锥




