题目内容
2.若直线mx-y+$\frac{n}{2}$-1=0(m>0,n>0)经过抛物线y2=4x的焦点,则$\frac{1}{m}$+$\frac{1}{n}$的最小值为( )| A. | 3+2$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3+\sqrt{2}}{2}$ |
分析 由抛物线y2=4x,可得焦点F(1,0),代入直线方程mx-y+$\frac{n}{2}$-1=0,可得:m+$\frac{n}{2}$=1.再利用“乘1法”与基本不等式即可得出最小值.
解答 解:由抛物线y2=4x,可得焦点F(1,0),
代入直线方程mx-y+$\frac{n}{2}$-1=0,
可得:m+$\frac{n}{2}$=1.
又m>0,n>0,
∴$\frac{1}{m}$+$\frac{1}{n}$=(m+$\frac{n}{2}$)($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{3}{2}$+$\frac{m}{n}$+$\frac{n}{2m}$
≥$\frac{3}{2}$+2$\sqrt{\frac{m}{n}•\frac{n}{2m}}$=$\frac{3+2\sqrt{2}}{2}$,
当且仅当n=$\sqrt{2}$m=2$\sqrt{2}$-2,取等号.
∴$\frac{1}{m}$+$\frac{1}{n}$的最小值是$\frac{3+2\sqrt{2}}{2}$.
故选C.
点评 本题考查了抛物线的性质、“乘1法”与基本不等式的性质,属于中档题和易错题.

练习册系列答案
相关题目
13.如图是函数y=f(x)的导函数y=f′(x)的图象,则下列判断正确的是( )


| A. | 在区间(-3,1)上y=f(x)是增函数 | B. | 在区间(1,3)上y=f(x)是减函数 | ||
| C. | 在区间(4,5)上y=f(x)是增函数 | D. | 在x=2时y=f(x)取到极小值 |
10.抛物线y2=4x图象上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线焦点为F,则△MPF的周长为( )
| A. | 5+$\sqrt{5}$ | B. | 5+2$\sqrt{5}$ | C. | 10 | D. | 10+2$\sqrt{5}$ |
7.抛物线x2=-8y的焦点坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (0,4) | D. | (0,-4) |
11.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
| A. | α∥β,m?α,n?β⇒m∥n | B. | m⊥α,m⊥n⇒n∥α | ||
| C. | α∩β=m,n∥α,n∥β⇒n∥m | D. | m?α,n?α,m∥β,n∥β⇒α∥β |

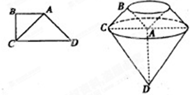 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周得到如图所示的几何体σ.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周得到如图所示的几何体σ.