题目内容
10.设把满足条件“对任意的s,t∈(一1,1)且s≠t.都有|f(s)-f(t)|≤3|s-t|”的函数f(x)组成的集合记作集合G.(1)分别判断函数f1(x)=$\sqrt{1+{x}^{2}}$,f2(x)=log2(1+x)是否属于集合G:
(2)若f3(x)=ax2+bx且f3(x)∈G.求证:当x∈(-2,2)时,|f3(x)|≤6.
分析 (1)由新定义判断函数f1(x)=$\sqrt{1+{x}^{2}}$,f2(x)=log2(1+x),是否满足对任意x1,x2∈(-1,1)时,都有|f(x1)-f(x2)|≤3|x1-x2|.运用分子有理化和绝对值不等式的性质,即可得到结论;
(2)由题意可得|f1(x1)-f1(x2)|≤3|x1-x2|,即有|x1-x2|•|a(x1+x2)+b|≤3|x1-x2|,即为|a(x1+x2)+b|≤3,再由绝对值不等式的性质,即可得证.
解答 解:(1)对于f1(x)=$\sqrt{1+{x}^{2}}$,对任意x1,x2∈(-1,1),
|f1(x1)-f1(x2)|=|$\sqrt{1+{{x}_{1}}^{2}}$-$\sqrt{1+{{x}_{2}}^{2}}$|=|$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{\sqrt{1+{{x}_{1}}^{2}}+\sqrt{1+{{x}_{2}}^{2}}}$|=|$\frac{{{(x}_{1}}^{\;}-{{x}_{2}}^{\;})({x}_{1}+{x}_{2})}{\sqrt{1+{{x}_{1}}^{2}}+\sqrt{1+{{x}_{2}}^{2}}}$|,$\sqrt{1+{{x}_{1}}^{2}}+\sqrt{1+{{x}_{2}}^{2}}$>|x1|+|x2|≥|x1+x2|
$\left|\frac{{{(x}_{1}}^{\;}-{{x}_{2}}^{\;})({x}_{1}+{x}_{2})}{\sqrt{1+{{x}_{1}}^{2}}+\sqrt{1+{{x}_{2}}^{2}}}\right|$<|x1-x2|<3|x1-x2|
|f1(x1)-f1(x2)|<3|x1-x2|
函数f1(x)=$\sqrt{1+{x}^{2}}$,属于集合G:
对于f(x)=log2(1+x)对任意x1,x2∈(-1,1),
|f1(x1)-f1(x2)|=|log2(1+x1)-log2(1+x2)|=|log2$\frac{1+{x}_{1}}{1+{x}_{2}}$|,
∵1+x1∈(0,2),1+x2∈(0,2),
$\frac{1+{x}_{1}}{1+{x}_{2}}∈[0,+∞)$,|log2$\frac{1+{x}_{1}}{1+{x}_{2}}$|∈R,不满足:|log2(1+x1)-log2(1+x2)|≤3|x1-x2|
故f2(x)=log2(1+x)不属于集合G.
(2)证明:f3(x)=ax2+bx且f3(x)∈G.
可得|f1(x1)-f1(x2)|≤3|x1-x2|,
即为|ax12+bx1-ax22-bx2|≤3|x1-x2|,
即有|x1-x2|•|a(x1+x2)+b|≤3|x1-x2|,
即为|a(x1+x2)+b|≤3,(x1,x2∈(-1,1))
当x∈(-2,2)时,|f3(x)|=|ax2+bx|=|x|•|ax+b|≤2×3=6,
则有当x∈(-2,2)时,|f3(x)|≤6.
点评 此题属于新概念的问题,题中考查了绝对值不等式的应用.对于此类型的题目需要对题目概念做认真分析再做题.属于中档题.

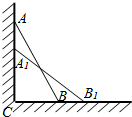 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.