题目内容
若方程
=x+m有两个不同的实数解，则m的取值范围是
| -x2-2x |
[2，1+
）
| 2 |
[2，1+
）
．| 2 |
分析：由题意得，函数y=
与函数y=x+m 有两个不同的交点，结合图象得出结果．
| -x2-2x |
解答：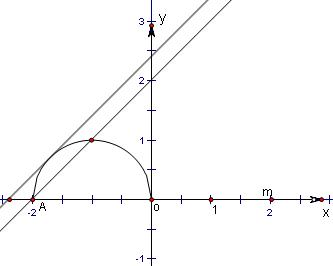
解：方程
=x+m有两个不同的实数解，即函数y=
与函数y=x+m 有两个不同的交点．
y=
的图象过圆心在（-1，0）半径为1的半圆，直线y=x+m 的图象斜率为1的平行直线系，如图所示：
故直线y=x+m在y轴上的截距m；-2≤a＜1+
，
故答案为[2，1+
）．
解：方程| -x2-2x |
| -x2-2x |
y=
| -x2-2x |
故直线y=x+m在y轴上的截距m；-2≤a＜1+
| 2 |
故答案为[2，1+
| 2 |
点评：本题考查方程根的个数的判断，体现了数形结合及转化的数学思想．
练习册系列答案
相关题目