题目内容
设a=(a1,a2),b=(b1,b2),定义一种向量积:a?b=(a1,b1)?(b1,b2)=(a1b1,a2b2).已知m=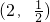 ,n=
,n= ,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别
,点P(x,y)在y=sin x的图象上运动,点Q在y=f(x)的图象上运动,且满足(x,f(x))=m?n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别
- A.2,π
- B.2,4π
- C.
 ,4π
,4π - D.
 ,π
,π
C
分析:先设出点P、Q的坐标,根据(x,f(x))=m?n得到P、Q的坐标之间的关系,从而写出函数f(x)的解析式得到答案.
解答:设P(x0,y0),Q(x,f(x)),
则由已知得(x,f(x))
=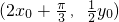 ,
,
即x=2x0+ ,
,
∴x0= x-
x- .
.
f(x)= y0,
y0,
∴y0=2f(x).又y0=sinx0,
∴2f(x)=sin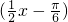 ,
,
f(x)= sin
sin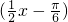 .
.
∴(f(x))max= ,
,
T=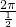
=4π.
点评:本题主要考查三角函数的最值和最小正周期的求法.这个题要先从条件中抽象出函数的解析式来,再解题.
分析:先设出点P、Q的坐标,根据(x,f(x))=m?n得到P、Q的坐标之间的关系,从而写出函数f(x)的解析式得到答案.
解答:设P(x0,y0),Q(x,f(x)),
则由已知得(x,f(x))
=
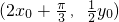 ,
,即x=2x0+
 ,
,∴x0=
 x-
x- .
.f(x)=
 y0,
y0,∴y0=2f(x).又y0=sinx0,
∴2f(x)=sin
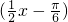 ,
,f(x)=
 sin
sin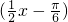 .
.∴(f(x))max=
 ,
,T=
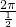
=4π.
点评:本题主要考查三角函数的最值和最小正周期的求法.这个题要先从条件中抽象出函数的解析式来,再解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目