题目内容
已知椭圆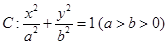 经过点
经过点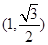 ,离心率为
,离心率为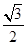 .
.
(1)求椭圆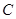 的方程;
的方程;
(2)直线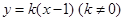 与椭圆
与椭圆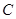 交于
交于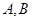 两点,点
两点,点 是椭圆
是椭圆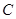 的右顶点.直线
的右顶点.直线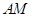 与直线
与直线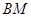 分别与
分别与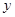 轴交于点
轴交于点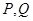 ,试问以线段
,试问以线段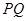 为直径的圆是否过
为直径的圆是否过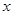 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
(1)椭圆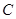 的方程是
的方程是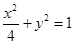 ;(2)线段
;(2)线段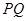 为直径的圆过
为直径的圆过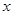 轴上的定点
轴上的定点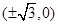 .
.
解析试题分析:(1)求椭圆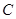 的方程,已知椭圆
的方程,已知椭圆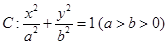 经过点
经过点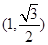 ,离心率为
,离心率为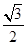 ,故可用待定系数法,利用离心率可得
,故可用待定系数法,利用离心率可得 ,利用过点
,利用过点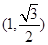 ,可得
,可得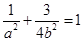 ,再由
,再由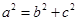 ,即可解出
,即可解出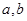 ,从而得椭圆
,从而得椭圆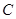 的方程;(2)这是探索性命题,可假设以线段
的方程;(2)这是探索性命题,可假设以线段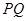 为直径的圆过
为直径的圆过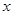 轴上的定点
轴上的定点 ,则
,则 ,故需表示出
,故需表示出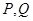 的坐标,因为点
的坐标,因为点 是椭圆
是椭圆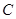 的右顶点,所以点
的右顶点,所以点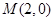 ,设
,设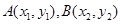 ,分别写出直线
,分别写出直线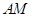 与的
与的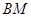 方程,得
方程,得 的坐标,由
的坐标,由 ,得
,得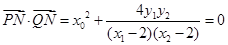 ,因此由
,因此由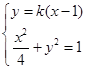 得
得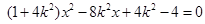 ,则
,则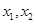 式方程的根,利用根与系数关系得,
式方程的根,利用根与系数关系得,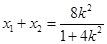 ,
,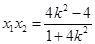 ,代入
,代入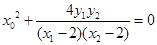 即可.
即可.
试题解析:(1)由题意得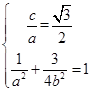 ,解得
,解得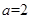 ,
,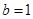 .
.
所以椭圆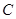 的方程是
的方程是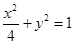 . 4分
. 4分
(2)以线段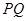 为直径的圆过
为直径的圆过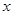 轴上的定点.
轴上的定点.
由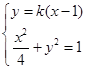 得
得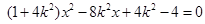 .
.
设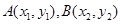 ,则有
,则有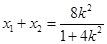 ,
,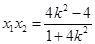 .
.
又因为点 是椭圆
是椭圆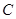 的右顶点,所以点
的右顶点,所以点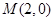 .
.
由题意可知直线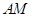 的方程为
的方程为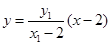 ,故点
,故点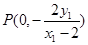 .
.
直线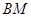 的方程为
的方程为 ,故点
,故点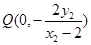 .
.
若以线段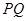 为直径的圆过
为直径的圆过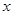 轴上的定点
轴上的定点 ,则等价于
,则等价于 恒成立.
恒成立.
又因为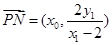 ,
,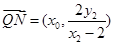 ,
,
所以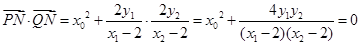 恒成立.
恒成立.
又因为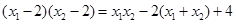
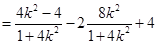
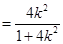 ,
,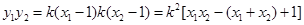
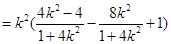
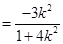 ,
,
所以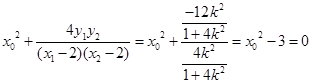 .解得
.解得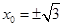 .
.
故以线段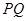 为直径的圆过
为直径的圆过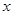 轴上的定点
轴上的定点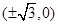 . 14分
. 14分
考点:求椭

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.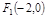 、
、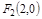 ,动点N满足
,动点N满足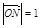 (O为坐标原点),
(O为坐标原点), ,
,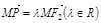 ,
,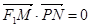 ,求点P的轨迹方程.
,求点P的轨迹方程. 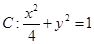 的上、下顶点分别为
的上、下顶点分别为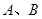 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点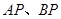 与直线
与直线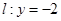 分别交于点
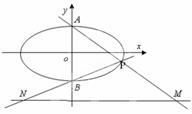
分别交于点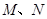 ,
,
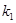 、
、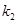 ,求证:
,求证: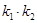 为定值;
为定值;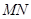 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论.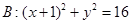 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。 :
: 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
 ,
, 是椭圆上异于
是椭圆上异于 分别交
分别交 轴于点
轴于点 ,若直线
,若直线 与过点
与过点 的圆
的圆 相切,切点为
相切,切点为 .证明:线段
.证明:线段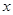 轴上的椭圆
轴上的椭圆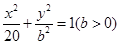 经过点
经过点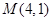 ,直线
,直线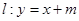
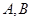 不同的两点.
不同的两点.
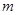 的取值范围;
的取值范围;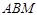 是以
是以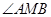 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出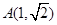 是离心率为
是离心率为 的椭圆
的椭圆 :
: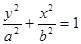
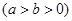 上的一点,斜率为
上的一点,斜率为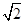 的直线
的直线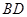 交椭圆
交椭圆 ,
, 两点,且
两点,且 、
、
 ,
, 的斜率之和为定值.
的斜率之和为定值. =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.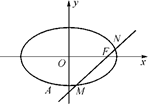
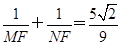 ,求实数m;
,求实数m;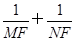 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.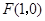 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点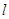 的垂线,垂足为点
的垂线,垂足为点 ,且
,且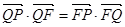 .
.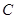 的方程;
的方程;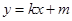 与曲线
与曲线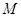 ,且与直线
,且与直线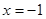 相交于点
相交于点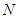 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点 ,使得以
,使得以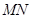 为直径的圆恒过此定点
为直径的圆恒过此定点