题目内容
已知f(x)=x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式.
【答案】
解析:设g(x)=x2+2ax+4,
由于关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
所以函数g(x)的图象开口向上且与x轴没有交点,
故Δ=4a2-16<0,∴-2<a<2. 又∵函数f(x)=(3-2a)x是增函数,∴3-2a>1,∴a<1.
解:∵函数图象的对称轴为x=-1,
(1)当t+1≤-1,即t≤-2时,
h(t)=f(t+1)=(t+1)2+2(t+1)-5,
即h(t)=t2+4t-2(t≤-2).
(2)当t≤-1<t+1,即-2<t≤-1时,
h(t)=f(-1)=-8.
(3)当t>-1时,h(t)=f(t)=t2+2t-5.
综上可得,h(t)=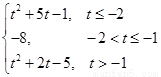
【解析】略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目