题目内容
已知|a|=3,|b|=2,a与b的夹角为60°,c=3a+5b,d=ma-3b.(1)当m为何值时,c与d垂直?
(2)当m为何值时,c与d共线?
思路分析：利用向量垂直,共线的充要条件构造关于m的方程求解.
解：(1)由向量垂直的充要条件,得c·d=0.
而c·d=(3a+5b)·(ma-3b)
=3ma2+(5m-9)a·b-15b2
=27m+3(5m-9)-60,
∴42m-87=0.
∴
,
即
时,c与d垂直.
(2)由向量共线的充要条件,得c=λd.
∴3a+5b=λ(ma-3b).
∴3a+5b=λma-3λb.
∵a与b不共线,
∴
解得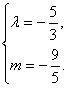
,
即当
时,c与d共线.
练习册系列答案
阅读快车系列答案
相关题目
,|b|=4,m=a+ b, n=a+λb,〈a, b〉=135°，m⊥n，则λ=____________
B.
C.4 D.-4