题目内容
如图,在三棱锥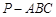 中,点
中,点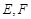 分别是棱
分别是棱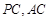 的中点.
的中点.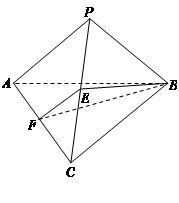
(1)求证: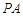 //平面
//平面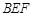 ;
;
(2)若平面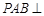 平面
平面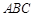 ,
,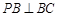 ,求证:
,求证: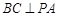 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)这是一个证明直线和平面平行的问题,考虑直线与平面平行的判定定理,可找面外线平行于面内线,本题容易找到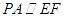 ,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.
,结论自然得证;(2)因为条件中有平面与平面垂直,故可考虑平面与平面垂直的判定定理,在一平面内作垂直于交线的直线平行于另一平面,再得到线线垂直,再证线面垂直,再得线线垂直,问题不难解决.
试题解析:(1)在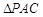 中,
中,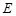 、
、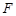 分别是
分别是 、
、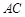 的中点,所以
的中点,所以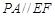 ,
,
又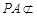 平面
平面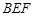 ,
,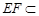 平面
平面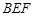 ,所以
,所以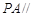 平面
平面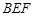 . 6分
. 6分
(2)在平面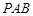 内过点
内过点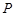 作
作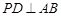 ,垂足为
,垂足为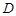 .因为平面
.因为平面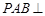 平面
平面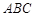 ,平面
,平面 平面
平面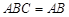 ,
,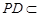 平面
平面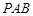 ,所以
,所以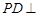 平面
平面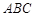 , 8分
, 8分
又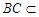 平面
平面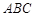 ,所以
,所以 , 10分
, 10分
又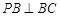 ,
,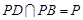 ,
,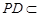 平面
平面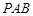 ,
,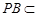 平面
平面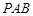 ,
,
所以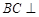 平面
平面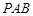 , 12分
, 12分
又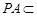 平面
平面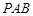 ,所以
,所以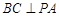 . 14分
. 14分
考点:直线与平面平行的判定、直线与平面垂直的判定,平面与平面垂直的性质.

练习册系列答案
相关题目
 平面
平面 ,
,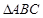 是等腰直角三角形,
是等腰直角三角形, ,四边形
,四边形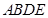 是直角梯形,
是直角梯形, ∥AE,
∥AE,
 ,
,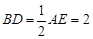 ,
, 分别为
分别为 的中点.
的中点.
 与
与 所成角的大小;
所成角的大小;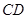 和平面
和平面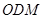 所成角的正弦值.
所成角的正弦值.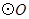 的直径
的直径 ,点
,点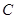 、
、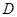 为
为 ,
,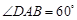 ,
,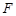 为弧
为弧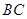 的中点.将
的中点.将 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).
 ;
;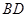 上是否存在点
上是否存在点 ,使得
,使得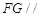 平面
平面 ?若存在,试指出点
?若存在,试指出点 的正弦值.
的正弦值.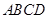 中,
中,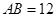 ,
,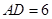 ,
,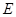 、
、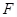 分别为
分别为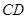 、
、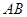 边上的点,且
边上的点,且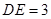 ,
,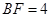 ,将
,将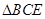 沿
沿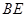 折起至
折起至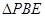 位置(如图2所示),连结
位置(如图2所示),连结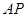 、
、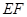 、
、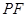 ,其中
,其中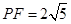 .
.
 平面
平面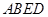 ;
;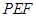 所成角的正弦值.
所成角的正弦值.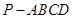 中,底面
中,底面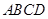 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且 交
交 于点
于点 .
.
 ;
; .
.
 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:
 ,求异面直线
,求异面直线 与
与 、
、 ,求三棱锥C1-BCA1的体积.
,求三棱锥C1-BCA1的体积. .
.
 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN