Question

6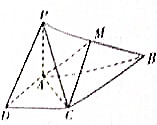．如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，AD=DC=$\frac{1}{2}$AB=1，PA⊥平面ABCD，异面直线AC与PB所成角的余弦值为$\frac{\sqrt{10}}{5}$，M为PB的中点，G为△AMC的重心．
（1）求证：BC⊥平面PAC；
（2）求DG与平面AMC所成角的正弦值．

Answer 1

分析 （1）首先根据已知条件，利用线段的值求出AC²+BC²=AB²，进一步利用线面垂直的性质定理，求出线线垂直，进一步得到线面垂直．
（2）利用异面直线夹角求出PA=1，进一步建立空间直角坐标系，利用法向量，求出线面的夹角的余弦值．

解答 证明：（1）已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，AD=DC=$\frac{1}{2}$AB=1，
利用勾股定理解得：BC=AC=$\sqrt{2}$，
所以：AC²+BC²=AB²
所以：AC⊥BC，
又PA⊥平面ABCD，
所以：PA⊥BC，
所以：BC⊥平面PAC．
（2）过点B作BE∥AC，交CD的延长线于点E，连接PE，设PA=x，
异面直线AC与PB所成角的余弦值为$\frac{\sqrt{10}}{5}$，
即：PB与BE所成角的余弦值为$\frac{\sqrt{10}}{5}$，
所以解得：$BE=\sqrt{2}$，AE=$\sqrt{10}$，$PB=\sqrt{{x}^{2}+4}$，$PE=\sqrt{{x}^{2}+10}$，
在△PBE中，COS∠PBE=$\frac{{PB}^{2}+{BE}^{2}-{PE}^{2}}{2•PB•BE}$，
解得：x=1，
即：PA=1．
建立空间直角坐标系：A-xyz，M为PB的中点，G为△AMC的重心．
则：A（0，0，0），P（0，0，1），B（0，2，0），D（1，0，0），C（1，1，0），
M（0，1，$\frac{1}{2}$），G（$\frac{1}{3}$，$\frac{2}{3}$，$\frac{1}{6}$），
则：$\overrightarrow{AM}=（0，1，\frac{1}{2}）$，$\overrightarrow{AC}=（1，1，0）$，$\overrightarrow{DG}=（-\frac{2}{3}，\frac{2}{3}，\frac{1}{6}）$．
设平面AMC的法向量为：$\overrightarrow{n}=（x，y，z）$，
则：$\left\{\begin{array}{l}\overrightarrow{AM}•\overrightarrow{n}=0\\ \overrightarrow{AC}•\overrightarrow{n}=0\end{array}\right.$，
解得：$\overrightarrow{n}=（-1，1，-2）$．
设DG与平面AMC所成角为θ，sinθ=$cos＜\overrightarrow{DG}，\overrightarrow{n}＞$=$\frac{\overrightarrow{DG}•\overrightarrow{n}}{\left|\overrightarrow{DG}\right|\left|\overrightarrow{n}\right|}$=$\frac{\sqrt{33}}{99}$
即：DG与平面AMC所成角的正弦值为$\frac{\sqrt{33}}{99}$．

点评 本题考查的知识要点：线面垂直的判定定理，异面直线的夹角的应用，空间直角坐标系，法向量，向量的数量积，线面的夹角的应用．及相关的运算问题．