题目内容

11．若tan（α+45°）＜0，则下列结论正确的是（　　）
A．sinx＜0B．cosx＜0C．sin2x＜0D．cos2x＜0

分析 求出角的范围，判断选项即可．

解答 解：tan（α+45°）＜0，
可得：k•180°+90°＜α+45°＜k•180°+180°，
即k•180°+45°＜α＜k•180°+135°
k•360°+90°＜2α＜k•360°+270°．
∴cos2x＜0．
故选：D．

点评 本题考查三角函数的角的范围的判断，三角函数值的符号，考查计算能力．

练习册系列答案
相关题目
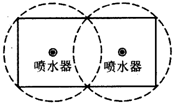1．某音乐喷泉喷射的水珠呈抛物线形，它在每分钟内随时间t（s）的变化规律大致可用y=-（1+4sin2$\frac{tπ}{60}$）x2+20（sin$\frac{tπ}{60}$）x（t为时间参数，x的单位为m）来描述，其中地面可作为x轴所在平面，泉眼为坐标原点，垂直于地面的直线为y轴．
（1）试求此喷泉喷射的圆形范围半径的最大值；
（2）若计划在一建筑物前维修一个矩形花坛并在花坛内装两个这样的喷泉（如图所示），如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？
2．若sin（$\frac{π}{6}$+a）=$\frac{1}{3}$，则cos（$\frac{π}{3}$-a）+cos（$\frac{2π}{3}$+a）-sin（$\frac{5π}{6}$-a）=-$\frac{1}{3}$．
19．若椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l（a＞b＞0）的离心率e=$\frac{3}{5}$，且椭圆C的一个焦点与抛物线y2=-12x的焦点重合．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点M（2，0），点Q是椭圆上一点．当|MQ|最小时，试求点Q的坐标；
（Ⅲ）设P（m，O）为椭圆C长轴（含端点）上的一个动点．过P点斜率为$\frac{4}{5}$的直线l交椭圆于A，B两点，设λ=
丨PA|2+|PB|2．试判断λ的取值是否与m有关，若有关，求出λ的取值范围；若无关，请说明理由．
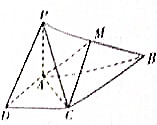6．如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，AD=DC=$\frac{1}{2}$AB=1，PA⊥平面ABCD，异面直线AC与PB所成角的余弦值为$\frac{\sqrt{10}}{5}$，M为PB的中点，G为△AMC的重心．
（1）求证：BC⊥平面PAC；
（2）求DG与平面AMC所成角的正弦值．
16．将函数y=f（x）的图象上每一点的纵坐标缩小为原来的$\frac{1}{2}$倍，再将横坐标压缩为原来的$\frac{1}{2}$倍，再将整个图象沿x轴向左平移$\frac{π}{3}$，可得y=sinx，则原来的函数f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{3}$）．
3．命题“?x∈R，3x-x3≤0”的否定是（　　）
A．?x∈R，3x-x3≥0B．?x∈R，3x-x3＞0C．?x∈R，3x-x3≥0D．?x∈R，3x-x3＞0
20．已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（{a＞b＞0}）的一个焦点为F（2，0），离心率为 $\frac{{\sqrt{6}}}{3}$．过焦点F 的直线l 与椭圆C交于 A，B两点，线段 AB中点为D，O为坐标原点，过O，D的直线交椭圆于M，N 两点．
（1）求椭圆C 的方程；
（2）求四边形AMBN 面积的最大值．
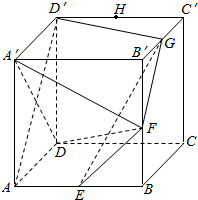7．在正方体ABCD-A′B′C′D′中，棱AB、BB′、B′C′、C′D′的中点分别是E，F，G，H，如图所示，则下列说法中正确的有（　　）
①点A，D′，H，F共面；
②直线EG与直线HF是异面直线；
③A′C⊥平面EFG；
④D′G∥平面A′DF．
A．①②B．②③C．②④D．③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网