题目内容
17.已知函数f(x)=x-alnx+$\frac{1+a}{x}$(a∈R)(1)求f(x)的单调区间;
(2)若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,求a的取值范围.
分析 (1)先求导,再分类讨论,得到函数的单调区间;
(2)由题意,只要求出函数f(x)min≤0即可,利用导数和函数的最值的关系,进行分类讨论,即可得到a的范围.
解答 解:(1)∵f(x)=x-alnx+$\frac{1+a}{x}$(a∈R),
∴f′(x)=1-$\frac{a}{x}$-$\frac{1+a}{{x}^{2}}$=$\frac{{x}^{2}-ax-(1+a)}{{x}^{2}}$=$\frac{(x+1)[x-(1+a)]}{{x}^{2}}$,
①当1+a≤0时,即a≤-1时,在x∈(0,+∞)上,f′(x)>0,
∴函数f(x)在(0,+∞)上单调递增,
②当a+1>0时,即a>-1时,在(0,1+a)上f′(x)<0,在(1+a,+∞)上,f′(x)>0,
∴函数f(x)在(0,1+a)上单调递减,在(1+a,+∞)上单调递增,
(2)在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立,
∴函数f(x)=x-alnx+$\frac{1+a}{x}$在[1,e]的最小值小于或等于0,
由(1)知,
当a≤-1时,在[1,e]上为增函数,f(x)min=f(1)=1+1+a≤0,
解得a≤-2,
当a>-1时
①当1+a≥e时,即a≥e-1时,f(x)在[1,e]上单调递减,
∴f(x)min=f(e)=e+$\frac{1+a}{e}$-a≤0,解得a≥$\frac{{e}^{2}+1}{e-1}$,
∵$\frac{{e}^{2}+1}{e-1}$>e-1,
∴a≥$\frac{{e}^{2}+1}{e-1}$;
②当1+a≤1,即a≤0,f(x)在[1,e]上单调递增,
∴f(x)min=f(1)=1+1+a≤0,
解得a≤-2,与a>-1矛盾;
③当1<1+a<e,即0<a<e-1时,f(x)min=f(1+a),
∵0<ln(1+a)<1,
∴0<aln(1+a)<a,
∴f(1+a)=a+2-aln(1+a)>2,此时f(1+a)≤0不成立,
综上所述若在[1,e](e=2.71828…)上任取一点x0,使得f(x0)≤0成立a的范围为a≥$\frac{{e}^{2}+1}{e-1}$,或a≤-2
点评 本题主要考查函数的单调性及最值,以及分类讨论的思想,转化思想,属于中档题.

| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
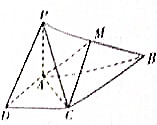 如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,AD=DC=$\frac{1}{2}$AB=1,PA⊥平面ABCD,异面直线AC与PB所成角的余弦值为$\frac{\sqrt{10}}{5}$,M为PB的中点,G为△AMC的重心.
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,AD=DC=$\frac{1}{2}$AB=1,PA⊥平面ABCD,异面直线AC与PB所成角的余弦值为$\frac{\sqrt{10}}{5}$,M为PB的中点,G为△AMC的重心.