题目内容
函数 在区间
在区间 上至少取得
上至少取得 个最大值,则正整数
个最大值,则正整数 的最小值是( )
的最小值是( )
A. | B. | C.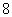 | D. |
C
解析试题分析:先根据函数的解析式求得函数的最小正周期,进而依据题意可推断出在区间上至少有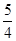 个周期.进而求得n≥6×
个周期.进而求得n≥6×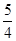 ,求得n的最小值.根据题意,由于函数
,求得n的最小值.根据题意,由于函数 的周期为
的周期为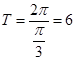 在区间[0,n]上至少取得2个最大值,说明在区间上至少有
在区间[0,n]上至少取得2个最大值,说明在区间上至少有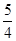 个周期.所以,n≥
个周期.所以,n≥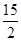 ∴正整数n的最小值是8故答案为C
∴正整数n的最小值是8故答案为C
考点:三角函数的周期性
点评:本题主要考查了三角函数的周期性及其求法.考查了考生对三角函数周期性的理解和灵活利用

练习册系列答案
相关题目
若 ,则
,则 ( )
( )
A. | B. | C. | D.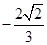 |
sin1,cos1,tan1的大小关系是( )
A. | B. |
C.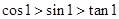 | D. |
将 的图象向左平移
的图象向左平移 个单位,得到
个单位,得到 的图象,则
的图象,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
函数 是
是
A.周期为 的奇函数 的奇函数 | B.周期为 的偶函数 的偶函数 |
C.周期为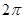 的奇函数 的奇函数 | D.周期为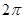 的偶函数 的偶函数 |
 等于( )
等于( )
A.- | B.- | C. | D. |
函数 的最小正周期是( )
的最小正周期是( )
A. | B.2 | C.4 | D. |
设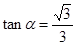 ,
,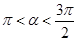 ,则
,则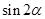 的值为( )
的值为( )
A.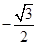 | B.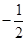 | C.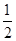 | D.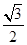 |
 在区间
在区间 上截直线
上截直线 及
及 所得的弦
所得的弦 ,则下列对
,则下列对 的描述正确的是( )
的描述正确的是( )


