Question

（05年浙江卷理）（14分）

已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x²－2x．

   (Ⅰ)求函数g(x)的解析式；

   (Ⅱ)解不等式g(x)≥f(x)－|x－1|．

Answer 1

解析：(Ⅰ)设函数y=f(x)的图象上任一点Q(x_q,y_q关于原点的对称点(x,y),

则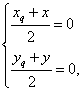即∵点Qx_q,y_q)在函数f(x)的图象上,

∴-y=-x²+2x.,故g(x)=-x²+2x

(Ⅱ)由g(x)≥f(x)－|x－1|可得2x²-|x-1|≤0,当x≥1时,2x²-x+1≤0,此时不等式无解,

当x<1时,2x²+x-1≤0,∴-1≤x≤,因此,原不等式的解集为[-1,]