题目内容
椭圆C: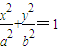 (a>b>0),A1、A2、B1、B2分别为椭圆C的长轴与短轴的端点.
(a>b>0),A1、A2、B1、B2分别为椭圆C的长轴与短轴的端点.(1)设点M(x,0),若当且仅当椭圆C上的点P在椭圆长轴顶点A1、A2处时,|PM|取得最大值与最小值,求x的取值范围;
(2)若椭圆C上的点P到焦点距离的最大值为3,最小值为l,且与直线l:y=kx+m相交于A,B两点(A,B不是椭圆的左右顶点),并满足AA2⊥BA2.试研究:直线l是否过定点?若过定点,请求出定点坐标,若不过定点,请说明理由.
【答案】分析:(1)先设出P点坐标,用P,M点坐标表示|PM|的平方,得到PM|的平方可看成是关于x的二次函数,再根据x的取值范围,求出PM|的平方的范围,进而得到x的取值范围.
(2)先根据椭圆C上的点P到焦点距离的最大值为3,最小值为l求出椭圆方程,再与直线l:y=kx+m联立,得到x1x2,x1+x2,再根据AA2⊥BA2,AA2与BA2斜率之积为-1,,求m的值,若能求出,则直线l过定点,若不能求出,则直线l不过定点.
解答:解:(1)设P(x,y)且 (a>b>0)
(a>b>0)
则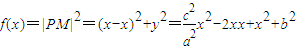 ,则对称轴方程为
,则对称轴方程为 ,
,
由题意只有当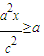 或
或 时满足题意,所以
时满足题意,所以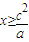 或
或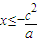
故x的取值范围是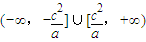 .
.
(2)因为 所以由(1)得:a+c=3,a-c=1,∴a=2,c=1,∴b2=a2-c2=3.
所以由(1)得:a+c=3,a-c=1,∴a=2,c=1,∴b2=a2-c2=3.
∴椭圆的标准方程为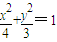 .
.
设A(x1,y1),B(x2,y2),联立
得(3+4k2)x2+8mkx+4(m2-3)=0,
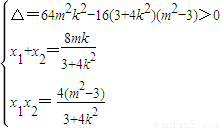
又y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2=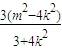 ,
,
因为椭圆的右顶点为A2(2,0),∴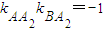 ,即
,即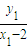
 =-1,
=-1,
y1y2+x1x2-2(x1+x2)+4=0,
∴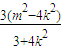 +
+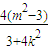 +
+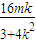 +4=0,∴7m2+16mk+4k2=0.
+4=0,∴7m2+16mk+4k2=0.
解得:m1=-2k,m2=- ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,
当m1=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当m2=- 时,l的方程为y=k(x-
时,l的方程为y=k(x- ),直线过定点(
),直线过定点( ,0).
,0).
所以,直线l过定点,定点坐标为( ,0).
,0).
点评:本题考查了直线与椭圆位置关系,计算量较大,做题时应认真,避免出错.
(2)先根据椭圆C上的点P到焦点距离的最大值为3,最小值为l求出椭圆方程,再与直线l:y=kx+m联立,得到x1x2,x1+x2,再根据AA2⊥BA2,AA2与BA2斜率之积为-1,,求m的值,若能求出,则直线l过定点,若不能求出,则直线l不过定点.
解答:解:(1)设P(x,y)且
 (a>b>0)
(a>b>0)则
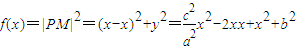 ,则对称轴方程为
,则对称轴方程为 ,
,由题意只有当
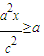 或
或 时满足题意,所以
时满足题意,所以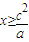 或
或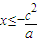
故x的取值范围是
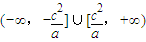 .
. (2)因为
 所以由(1)得:a+c=3,a-c=1,∴a=2,c=1,∴b2=a2-c2=3.
所以由(1)得:a+c=3,a-c=1,∴a=2,c=1,∴b2=a2-c2=3.∴椭圆的标准方程为
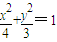 .
. 设A(x1,y1),B(x2,y2),联立

得(3+4k2)x2+8mkx+4(m2-3)=0,
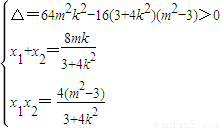
又y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2=
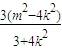 ,
,因为椭圆的右顶点为A2(2,0),∴
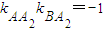 ,即
,即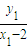
 =-1,
=-1,y1y2+x1x2-2(x1+x2)+4=0,
∴
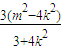 +
+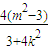 +
+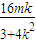 +4=0,∴7m2+16mk+4k2=0.
+4=0,∴7m2+16mk+4k2=0.解得:m1=-2k,m2=-
 ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,当m1=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当m2=-
 时,l的方程为y=k(x-
时,l的方程为y=k(x- ),直线过定点(
),直线过定点( ,0).
,0).所以,直线l过定点,定点坐标为(
 ,0).
,0).点评:本题考查了直线与椭圆位置关系,计算量较大,做题时应认真,避免出错.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
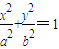 (a>b>0)的长轴长是短轴长的两倍,焦距为
(a>b>0)的长轴长是短轴长的两倍,焦距为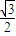 .
.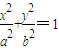 (a>b>0).
(a>b>0).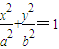 (a>b>0)的短轴的一个端点,F为椭圆C的一个焦点,O为坐标原点,记∠BFO=θ.当椭圆C同时满足下列两个条件:①
(a>b>0)的短轴的一个端点,F为椭圆C的一个焦点,O为坐标原点,记∠BFO=θ.当椭圆C同时满足下列两个条件:①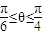 ;②a2+b2=2a2b2.求椭圆长轴的取值范围.
;②a2+b2=2a2b2.求椭圆长轴的取值范围.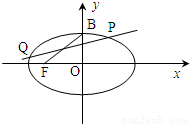
 +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。