题目内容
函数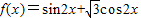
的最大值记为M，周期为
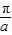，则函数g（t）=t2（t-a）在区间[0，M]上的最大值为（ ）A．1
B．0
C．
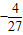
D．4
【答案】分析：利用两角和的正弦公式化简函数解析式为2sin（2x+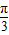
），由此求得最大值M，根据周期的值求出a的值，利用导数求
出函数g（t）=t2（t-1）在[0，2]上的最大值．
解答：解：∵函数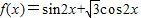
=2（
）=2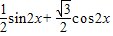sin（2x+
），
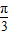故函数的最大值M=2，周期为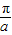
=
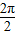，∴a=1．
故函数g（t）=t2（t-a）=t2（t-1），区间[0，M]即[0，2]．
g′（t）=3t2-2t，故当t∈（0，
）上时，g′（t）＜0，当t∈（
，2]上时，g′（t）＞0．
故函数在∈（0，
）上是减函数，在∈（
，2]上是增函数．
故函数的最大值为g（0）或g（2）．
再由g（0）=0，g（2）=4 可得，函数g（t）=t2（t-a）在区间[0，M]上的最大值为4，
故选D．
点评：本题主要考查两角和的正弦公式，正弦函数的周期性，利用导数求函数在闭区间上的最大值，属于中档题．
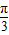），由此求得最大值M，根据周期的值求出a的值，利用导数求出函数g（t）=t2（t-1）在[0，2]上的最大值．
解答：解：∵函数
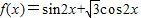=2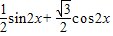（）=2sin（2x+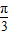），故函数的最大值M=2，周期为
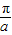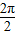=，∴a=1．故函数g（t）=t2（t-a）=t2（t-1），区间[0，M]即[0，2]．
g′（t）=3t2-2t，故当t∈（0，
）上时，g′（t）＜0，当t∈（，2]上时，g′（t）＞0．故函数在∈（0，
）上是减函数，在∈（，2]上是增函数．故函数的最大值为g（0）或g（2）．
再由g（0）=0，g（2）=4 可得，函数g（t）=t2（t-a）在区间[0，M]上的最大值为4，
故选D．
点评：本题主要考查两角和的正弦公式，正弦函数的周期性，利用导数求函数在闭区间上的最大值，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=-x2+2tx-4在闭区间[0，1]上的最大值记为g（t）