题目内容
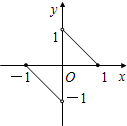 f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)<1 的解集是
f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)<1 的解集是[-1, 0)∪(
, 1]
| 1 |
| 2 |
[-1, 0)∪(
, 1]
.| 1 |
| 2 |
分析:如图可以看出f(x)为奇函数,得f(-x)=-f(x),利用数形结合的方法进行求解;
解答:解:∵f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],
由图象可知:f(x)为奇函数,f(-x)=-f(x),
∴不等式f(x)-f(-x)<1,2f(x)<1,f(x)<
,
当-1<x<0时,f(x)<0<
,
当0<x<1时,y=1-x,1-x<
,x>
,
∴
<x<1,
∴不等式f(x)-f(-x)<1 的解集是:[-1, 0)∪(
, 1];
由图象可知:f(x)为奇函数,f(-x)=-f(x),
∴不等式f(x)-f(-x)<1,2f(x)<1,f(x)<
| 1 |
| 2 |
当-1<x<0时,f(x)<0<
| 1 |
| 2 |
当0<x<1时,y=1-x,1-x<
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴不等式f(x)-f(-x)<1 的解集是:[-1, 0)∪(
| 1 |
| 2 |
点评:此题主要考查函数的图象,此题利用数形结合的方法,这种思想对于做选择题和填空题很有用,是一道好题.

练习册系列答案
相关题目
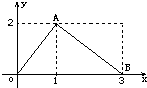 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )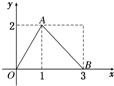 函数f(x)的图象是如图所示的折线段OAB,其中点A(1,2)、B(3,0),函数g(x)=(x-1)f(x),则函数g(x)的最大值为
函数f(x)的图象是如图所示的折线段OAB,其中点A(1,2)、B(3,0),函数g(x)=(x-1)f(x),则函数g(x)的最大值为
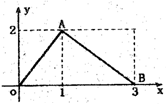 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为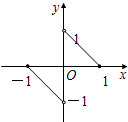 f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)>0的解集是
f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)>0的解集是