题目内容
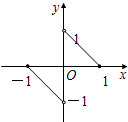 f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)>0的解集是
f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)>0的解集是(0,1)
(0,1)
.分析:根据图象求出x∈(0,1]时,f(x)=-x+1,求得x∈[-1,0)时,f(x)=-x-1,利用奇函数,要求不等式f(x)-f(-x)>0的解集,即求f(x)>0,通过函数的图象即可求得结果.
解答:解:∵函数f(x)的定义域是[-1,0)∪(0,1],由图象知x∈(0,1]时,f(x)=-x+1
∴x∈[-1,0)时,f(x)=-x-1,函数是奇函数,
∵f(x)-f(-x)>0,∴2f(x)>0,
通过函数的图象可知,当x∈(0,1)时恒成立,
故答案为:(0,1).
∴x∈[-1,0)时,f(x)=-x-1,函数是奇函数,
∵f(x)-f(-x)>0,∴2f(x)>0,
通过函数的图象可知,当x∈(0,1)时恒成立,
故答案为:(0,1).
点评:此题考查函数的奇偶性和图象的综合题.考查学生的识图能力,根据函数的奇偶性和图象写出函数的解析式是解题的关键,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
相关题目
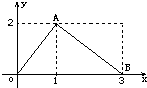 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0).定义函数g(x)=f(x)•(x-1).则函数g(x)最大值为( )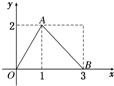 函数f(x)的图象是如图所示的折线段OAB,其中点A(1,2)、B(3,0),函数g(x)=(x-1)f(x),则函数g(x)的最大值为
函数f(x)的图象是如图所示的折线段OAB,其中点A(1,2)、B(3,0),函数g(x)=(x-1)f(x),则函数g(x)的最大值为
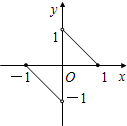 f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)<1 的解集是
f(x)的图象是如图两条线段,它的定义域是[-1,0)∪(0,1],则不等式f(x)-f(-x)<1 的解集是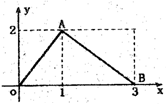 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),定义函数g(x)=f(x)•x,则函数g(x)最大值为