题目内容
16．
如图，△ABC为直角三角形，∠BAC=90°，PA⊥平面ABC，A为垂足．PC与底面成30°角，且AB=a，AC=2a．（1）求点A到平面PBC的距离；
（2）求二面角A-PC-B的大小．
分析 （1）过A作AE⊥PC，垂足为E，连接BE，作AH⊥BE，垂足为H，证明AH⊥平面PBC，即可求点A到平面PBC的距离；
（2）由（1）知，∠BEA为二面角A-PC-B的平面角，即可求二面角A-PC-B的大小．
解答 解：（1）过A作AE⊥PC，垂足为E，连接BE，作AH⊥BE，垂足为H，则
∵∠BAC=90°，
∴BA⊥AC，
∵PA⊥平面ABC，BA?平面ABC，
∴BA⊥PA，
∵PA∩AC=A，
∴BA⊥平面PAC，
∵AE⊥PC，
∴BE⊥PC，
∵AE⊥PC，AE∩BE=E，
∴PC⊥平面ABE，
∴PC⊥AH，
∵AH⊥BE，PC∩BE=E，
∴AH⊥平面PBC
Rt△EAC中，∠ECA=30°，AC=2a，∴AE=a，
Rt△EAB中，AB=a，∴AH=$\frac{\sqrt{2}}{2}$a，
∴点A到平面PBC的距离为$\frac{\sqrt{2}}{2}$a；
（2）由（1）知，∠BEA为二面角A-PC-B的平面角，且∠BEA=45°．
点评 本题考查二面角A-PC-B的平面角、点A到平面PBC的距离，考查学生分析解决问题的能力，证明AH⊥平面PBC
是关键．
练习册系列答案
相关题目
7．自驾游从A地到B地有甲乙两条线路，甲线路是A-C-D-B，乙线路是A-E-F-G-H-B，其中CD段、EF段、GH段都是易堵车路段．假设这三条路段堵车与否相互独立．这三条路段的堵车概率及平均堵车时间如表1所示．
经调查发现，堵车概率x在（$\frac{2}{3}$，1）上变化，y在（0，$\frac{1}{2}$）上变化．
在不堵车的情况下．走线路甲需汽油费500元，走线路乙需汽油费545元．而每堵车1小时，需多花汽油费20元．路政局为了估计CD段平均堵车时间，调查了100名走甲线路的司机，得到表2数据．
（1）求CD段平均堵车时间a的值．
（2）若只考虑所花汽油费期望值的大小，为了节约，求选择走甲线路的概率．
（3）在（2）的条件下，某4名司机中走甲线路的人数记为X，求X的数学期望．
经调查发现，堵车概率x在（$\frac{2}{3}$，1）上变化，y在（0，$\frac{1}{2}$）上变化．
在不堵车的情况下．走线路甲需汽油费500元，走线路乙需汽油费545元．而每堵车1小时，需多花汽油费20元．路政局为了估计CD段平均堵车时间，调查了100名走甲线路的司机，得到表2数据．
| 堵车时间（单位：小时） | 频数 |
| [0，1] | 8 |
| （1，2] | 6 |
| （2，3] | 38 |
| （3，4] | 24 |
| （4，5] | 24 |
| （表2） | |
| CD段 | EF段 | GH段 | |
| 堵车概率 | x | y | $\frac{1}{4}$ |
| 平均堵车时间 （单位：小时） | a | 2 | 1 |
| （表1） | |||
（2）若只考虑所花汽油费期望值的大小，为了节约，求选择走甲线路的概率．
（3）在（2）的条件下，某4名司机中走甲线路的人数记为X，求X的数学期望．
如图，AB是圆O的直径，点C在圆O上，矩形DCBE所在的平面垂直于圆O所在的平面，AB=4，BE=1．
11．
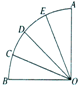扇形AOB的半径为1，圆心角为90°，点C、D、E将弧AB分成四等分，连结OC、OD、OE，从图中所有的扇形中随机取出一个，面积恰好为$\frac{π}{8}$的概率是（ ）
扇形AOB的半径为1，圆心角为90°，点C、D、E将弧AB分成四等分，连结OC、OD、OE，从图中所有的扇形中随机取出一个，面积恰好为$\frac{π}{8}$的概率是（ ）| A． | $\frac{3}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．