题目内容
已知函数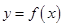 的大致图象如图所示,则函数
的大致图象如图所示,则函数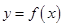 的解析式应为
的解析式应为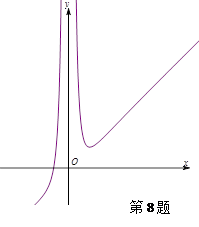
A.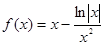 | B.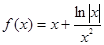 |
C.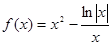 | D.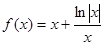 |
A
解析考点:函数的图象;函数解析式的求解及常用方法.
分析:函数y=f(x)的解析求不出来,根据选项结合图象采用排除法进行排除,以及利用特殊值法进行排除.
解:根据图象不关于原点对称,则该函数不是奇函数,可排除选项D,
取x=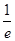 时,根据图象可知函数值大于0,而选项B,f(
时,根据图象可知函数值大于0,而选项B,f(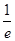 )=
)=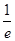 +
+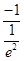 =
=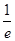 -e2<0,故B不正确,
-e2<0,故B不正确,
由题上图象可以看出当x→-∞时,有f(x)<0,
但C选项,f(x)=x2-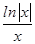 ,当x→-∞时,f(x)=x2-
,当x→-∞时,f(x)=x2-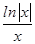 >0,
>0,
∴C错误
故选A.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
抛物线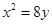 的准线方程为( )
的准线方程为( )
A.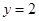 | B.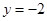 | C.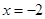 | D.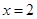 |
抛物线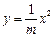 的焦点坐标为( )
的焦点坐标为( )
A. | B.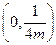 | C.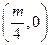 | D.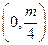 |
直角坐标系中,抛物线x2=-3y经过伸缩变换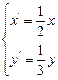 后得曲线( )
后得曲线( )
| A.y′2=-4x′ | B.x′2=-4y′ |
| C.y′2=-x′ | D.x′2=-y′ |
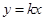 与椭圆
与椭圆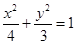 相交于
相交于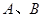 两点,分别过
两点,分别过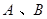 向
向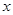 轴作垂线,若垂足恰为椭圆的两个焦点,则
轴作垂线,若垂足恰为椭圆的两个焦点,则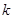 等于( ).
等于( ).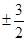
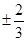
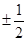
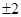
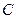 :
: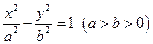 和圆
和圆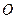 :
: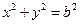 (其中原点
(其中原点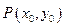 引圆
引圆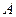 、
、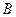 .
. 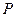 ,使得
,使得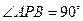 ,求双曲线离心率
,求双曲线离心率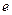 的取值范围;
的取值范围; 求直线
求直线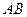 的方程;
的方程;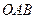 面积的最大值.
面积的最大值. (a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则
(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则 等于 ( )
等于 ( ) C
C
 D
D
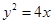 的焦点F作直线
的焦点F作直线 交抛物线于A,B两点,若
交抛物线于A,B两点,若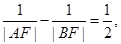 则直线
则直线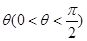 等于( )
等于( )
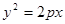 的焦点与椭圆
的焦点与椭圆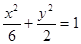 的右焦点重合,则
的右焦点重合,则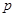 的值为 ( )
的值为 ( )