题目内容
设直线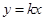 与椭圆
与椭圆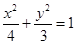 相交于
相交于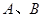 两点,分别过
两点,分别过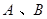 向
向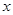 轴作垂线,若垂足恰为椭圆的两个焦点,则
轴作垂线,若垂足恰为椭圆的两个焦点,则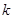 等于( ).
等于( ).
A.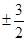 | B.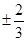 | C.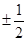 | D.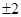 |
A
解析考点:直线与圆锥曲线的关系.
分析:将直线方程与椭圆方程联立,得(3+4k2)x2=12.分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,说明A,B的横坐标是±1,即方程(3+4k2)x2=12的两个根为±1,代入求出k的值.
解:将直线与椭圆方程联立,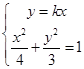 ,
,
化简整理得(3+4k2)x2=12(*)
因为分别过A、B向x轴作垂线,垂足恰为椭圆的两个焦点,
故方程的两个根为±1.代入方程(*),得k=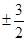
故选A.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
在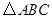 中,
中,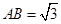 ,
,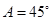 ,
,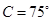 ,则
,则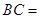 ( )
( )
A.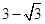 | B.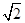 | C.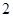 | D.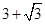 |
已知函数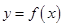 的大致图象如图所示,则函数
的大致图象如图所示,则函数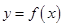 的解析式应为
的解析式应为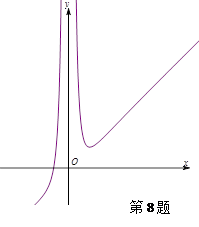
A.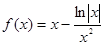 | B.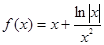 |
C.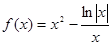 | D.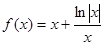 |
双曲线 的离心率
的离心率 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A.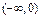 | B. |
C.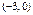 | D.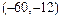 |
抛物线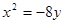 的准线方程是( ).
的准线方程是( ).
A.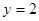 | B.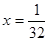 | C.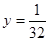 | D.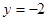 |
焦点为F(0,10),渐近线方程为4x±3y=0的双曲线的方程是 ( )
A.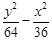 =1 =1 | B.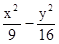 =1 =1 | C.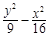 ="1" ="1" | D.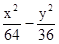 =1 =1 |
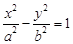 (a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
(a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为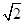

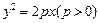 的焦点
的焦点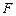 为双曲线
为双曲线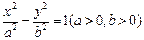 的一个焦点,经过两曲线交点的直线恰好过点
的一个焦点,经过两曲线交点的直线恰好过点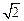

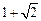
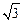

 的曲线大致是 ( )
的曲线大致是 ( )