Question

已知定义在[1，+∞）上的函数f（x）=

4-|8x-12|，1≤x≤2 1 2 f( x 2 )，x＞2

，则（　　）

A．函数f（x）的值域为[1，4]

B．关于x的方程f（x）- 1 2n =0（n∈N*）有2n+4个不相等的实数根

C．当x∈[2n-1，2n]（n∈N*）时，函数f（x）的图象与x轴围成的面积为2

D．存在实数x0，使得不等式x0f（x0）＞6成立

Answer 1

①当1≤x≤

3

2

时，f（x）=8x-8，此时，0≤f（x）≤4；当

3

2

＜x≤2时，f（x）=16-8x，此时，0≤f（x）＜4；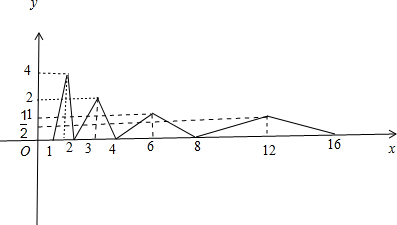
②当2＜x≤3时，则1＜

x

2

≤

3

2

，此时f（x）=

1

2

(8×

x

2

-8)=8×

x

22

-4=2x-4，此时，0≤f（x）≤2；
当3＜x≤4时，则

3

2

＜

x

2

≤2，此时f（x）=

1

2

(16-8×

x

2

)=8-8×

x

22

，此时，0≤f（x）＜2；
…，
依此类推：当2^n-1≤x≤3•2^n-2时，f（x）=

23-n

3×2n-2-2n-1

(x-2n-1)=2^5-2n（x-2^n-1），
此时，0≤f（x）≤2^3-n；当3•2^n-2＜x≤2ⁿ时，f（x）=-2^5-2n（x-2ⁿ），此时，0≤f（x）≤2^3-n．
据此可得：函数f（x）的值域为[0，4]，故A不正确；当n=1时，f(x)=

1

2

，有且仅有7个不等实数根，不是2×1+4=6个不等实数根，故B不正确；当x∈[2^n-1，2ⁿ]（n∈N^*）时，函数f（x）的图象与x轴围成的面积S=

1

2

×(2n-2n-1)×23-n=2，故C正确；xf（x）＞6?f(x)＞

6

x

，由f（x）的图象可得到：当x∈[2^n-1，2ⁿ]（n∈N^*）时，f(x)≤f(3•2n-2)=23-n=

6

3•2n-2

可得：f(x)≤

6

x

，故D不正确．
综上可知：只有C正确．
故选C．