题目内容
在△ABC中，角A,B,C所对的边分别为a,b,c，且满足csinA=acosC．
（1）求角C的大小；
（2）求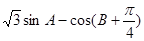
的最大值，并求取得最大值时角A、B的大小.
【答案】
解：（I）由正弦定理得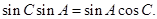
因为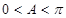
，所以sinA>0,从而sinC=cosC.
又cosC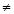
0,所以tanC=1,则C=
.
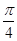（II）由（I）知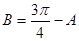
于是
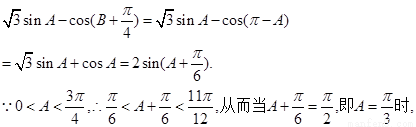
2sin(A+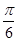
)取最大值2．
综上所述，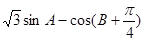
的最大值为2，此时
.
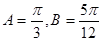【解析】略
练习册系列答案
初中暑期衔接系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |