题目内容
已知函数f(x)=Asinωx+Bcosωx(A、B、ω是实常数,ω>0)的最小正周期为2,并当x= 时,f(x)max=2.
时,f(x)max=2.(1)求f(x).
(2)在闭区间[
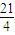 ,
,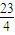 ]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,请说明理由.
【答案】分析:(1)先根据最小正周期求出w的值,再由当x= 时,f(x)max=2和三角函数的性质可求出A,B的值,进而得到函数f(x)的解析式.
时,f(x)max=2和三角函数的性质可求出A,B的值,进而得到函数f(x)的解析式.
(2)令πx+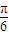 =kπ+
=kπ+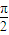 求出x的值,再根据x的范围确定k的范围,最后由k为整数可确定答案.
求出x的值,再根据x的范围确定k的范围,最后由k为整数可确定答案.
解答:解:(1)∵T=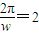 ,∴w=π
,∴w=π
A2+B2=4,Asin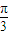 +Bcos
+Bcos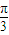 =
=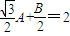
∴A=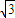 ,B=2
,B=2
∴f(x)=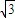 sinπx+cosπx=2sin(πx+
sinπx+cosπx=2sin(πx+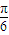 ).
).
(2)令πx+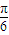 =kπ+
=kπ+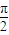 ,k∈Z.
,k∈Z.
∴x=k+ ,
,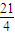 ≤k+
≤k+ ≤
≤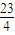 .
.
∴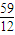 ≤k≤
≤k≤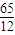 .
.
∴k=5.
故在[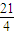 ,
,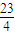 ]上只有f(x)的一条对称轴x=
]上只有f(x)的一条对称轴x=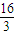 .
.
点评:本题主要考查三角函数的最小正周期的求法和对称轴的求法.三角函数的基础知识是解题的关键,要熟练掌握.
 时,f(x)max=2和三角函数的性质可求出A,B的值,进而得到函数f(x)的解析式.
时,f(x)max=2和三角函数的性质可求出A,B的值,进而得到函数f(x)的解析式.(2)令πx+
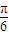 =kπ+
=kπ+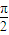 求出x的值,再根据x的范围确定k的范围,最后由k为整数可确定答案.
求出x的值,再根据x的范围确定k的范围,最后由k为整数可确定答案.解答:解:(1)∵T=
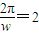 ,∴w=π
,∴w=πA2+B2=4,Asin
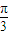 +Bcos
+Bcos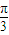 =
=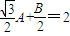
∴A=
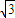 ,B=2
,B=2∴f(x)=
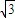 sinπx+cosπx=2sin(πx+
sinπx+cosπx=2sin(πx+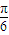 ).
).(2)令πx+
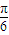 =kπ+
=kπ+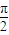 ,k∈Z.
,k∈Z.∴x=k+
 ,
,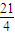 ≤k+
≤k+ ≤
≤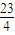 .
.∴
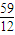 ≤k≤
≤k≤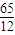 .
.∴k=5.
故在[
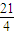 ,
,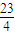 ]上只有f(x)的一条对称轴x=
]上只有f(x)的一条对称轴x=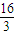 .
.点评:本题主要考查三角函数的最小正周期的求法和对称轴的求法.三角函数的基础知识是解题的关键,要熟练掌握.

练习册系列答案
相关题目