题目内容
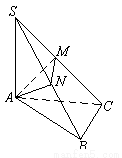
 在空间四边形SABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
在空间四边形SABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2| 3 |
(1)证明:AC⊥SB;
(2)求二面角N-CM-B的大小.
分析:(1)欲证AC⊥SB,取AC中点D,连接DS、DB.根据线面垂直的性质定理可知,只须证AC⊥SD且AC⊥DB,即得;
(2)欲求二面角N-CM-B的大小,可先作出二面角的平面角,结合SD⊥平面ABC.过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连接NF,则NF⊥CM.可得∠NFE为二面角N-CM-B的平面角.最后在Rt△NEF中求解即可得到答案.
(2)欲求二面角N-CM-B的大小,可先作出二面角的平面角,结合SD⊥平面ABC.过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连接NF,则NF⊥CM.可得∠NFE为二面角N-CM-B的平面角.最后在Rt△NEF中求解即可得到答案.
解答:解:(1)取AC中点D,连接SD、DB.
∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD,
∴AC⊥平面SDB,
又∵SB?平面SDB,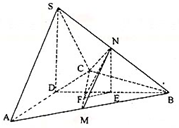
∴AC⊥SB.
(2)∵AC⊥平面SDB,AC?平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连接NF,则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角.
∵平面SAC⊥平面ABC,SD⊥AC,
∴SD⊥平面ABC.
又∵NE⊥平面ABC,
∴NE∥SD.
∵SN=NB,
∴NE=
SD=
=
=
,且ED=EB.
在正△ABC中,由平几知识可求得EF=
MB=
,
在Rt△NEF中,tan∠NFE=
=2
,
∴二面角N-CM-B的大小是arctan2
.
∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD,
∴AC⊥平面SDB,
又∵SB?平面SDB,

∴AC⊥SB.
(2)∵AC⊥平面SDB,AC?平面ABC,
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连接NF,则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角.
∵平面SAC⊥平面ABC,SD⊥AC,
∴SD⊥平面ABC.
又∵NE⊥平面ABC,
∴NE∥SD.
∵SN=NB,
∴NE=
| 1 |
| 2 |
| 1 |
| 2 |
| SA2-AD2 |
| 1 |
| 2 |
| 12-4 |
| 2 |
在正△ABC中,由平几知识可求得EF=
| 1 |
| 4 |
| 1 |
| 2 |
在Rt△NEF中,tan∠NFE=
| EN |
| EF |
| 2 |
∴二面角N-CM-B的大小是arctan2
| 2 |
点评:本小题主要考查直线与直线、直线与平面的位置关系,以及二面角的做法与求法,考查空间想象能力和逻辑推理能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 如图,在空间四边形SABC中,AC、BS为其对角线,O为△ABC的重心,
如图,在空间四边形SABC中,AC、BS为其对角线,O为△ABC的重心,

 (;(2)
(;(2) .
. 平面ABC,
平面ABC, 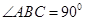 ,
,  于N,
于N, 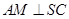 于M.
于M.