题目内容
已知二次函数,y=g(x)的图象过(0,0),(m,0)(m+1,m+1)三点.
(1)求y=g(x)的表达式;
(2)设f(x)=(x-n)·g(x),(m>n>0)且在x=a和x=b,(b<a)处取到极值.①求证:0<b<n<a<m.②若m+n<![]() ,则过原点且与曲线y=f(x)相切的两条直线,能否互相垂直,给予证明.
,则过原点且与曲线y=f(x)相切的两条直线,能否互相垂直,给予证明.
答案:
解析:
解析:
|
(1)设g(x)=Ax(x-m),过(m+1,m+1) ∴A=1,则g(x)=x(x-m) (2)①f(x)=(x-n)(x-m)·x=x3-(m+n)x2+mn·x 又∵f(x)在x=a,x=b取极值 设 3(m-a)(m-b)>0 a<m或m<b(舍) 同理 ②x0=0,x0= k1=mn,k2= k1·k2=-1 即mn 而实际 ∴不可能 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
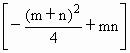
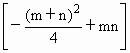 =-1,
=-1,