题目内容
设全集Y=R,A={ x|-1<x+1<2},函数y= 的定义域为B,求
的定义域为B,求(1)A∩B;
(2)CU(A∪B).
【答案】分析:求出集合A中不等式的解集,确定出A,求出函数的定义域,确定出B,
(1)找出两集合的公共部分,即可求出两集合的交集;
(2)找出既属于A又属于B的部分,确定出两集合的并集,找出全集中不属于A与B并集的部分,即可确定出所求的集合.
解答:解:由集合A中的不等式解得:-2<x<1,即A=(-2,1);
由函数解析式得:2x-1>0,即x> ,即B=(
,即B=( ,+∞),
,+∞),
(1)A∩B=( ,1);
,1);
(2)∵A∪B=(-2,+∞),全集U=R,
∴CU(A∪B)=(-∞,2].
点评:此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.
(1)找出两集合的公共部分,即可求出两集合的交集;
(2)找出既属于A又属于B的部分,确定出两集合的并集,找出全集中不属于A与B并集的部分,即可确定出所求的集合.
解答:解:由集合A中的不等式解得:-2<x<1,即A=(-2,1);
由函数解析式得:2x-1>0,即x>
 ,即B=(
,即B=( ,+∞),
,+∞),(1)A∩B=(
 ,1);
,1);(2)∵A∪B=(-2,+∞),全集U=R,
∴CU(A∪B)=(-∞,2].
点评:此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.

练习册系列答案
相关题目
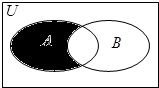 (2012•蓝山县模拟)设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
(2012•蓝山县模拟)设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )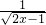 的定义域为B,求
的定义域为B,求