Question

12．已知直角梯形ABCD如图1所示，CD=2，AB=4，AD=2，线段AB上有一点P，过点P作AB的垂线交l，当点P从点A运动到点B时，记AP=x，l截直角梯形的左边部分面积为S（x），
（1）试写出S（x）关于x的函数，并在图2中画出函数图象．
（2）当点P位于何处时，S（x）为直角梯形ABCD面积的$\frac{3}{4}$？

Answer 1

分析 （1）可看出当l在过C前和过C后面积S（x）的求法不同，从而分0≤x≤2和2＜x≤4两种情况求面积S（x）=$\left\{\begin{array}{l}{2x}&{0≤x≤2}\\{-\frac{1}{2}（x-4）^{2}+6}&{2＜x≤4}\end{array}\right.$，然后根据S（x）的解析式画出图象即可；
（2）容易求出直角梯形ABCD的面积，从而得出S（x）=$\frac{9}{2}$，从而可以判断出2＜x＜4，从而解方程$-\frac{1}{2}（x-4）^{2}+6=\frac{9}{2}$便可求出x，从而得出点P的位置．

解答 解：（1）0≤x≤4；
①当0≤x≤2时，S（x）=2x；
②当2＜x≤4时，$S（x）=4+\frac{（4-x+2）（x-2）}{2}=-\frac{1}{2}（x-4）^{2}+6$；
∴$S（x）=\left\{\begin{array}{l}{2x}&{0≤x≤2}\\{-\frac{1}{2}（x-4）^{2}+6}&{2＜x≤4}\end{array}\right.$；
S（x）的图象如下：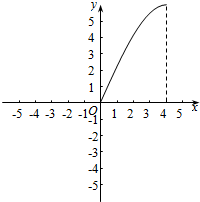

（2）直角梯形ABCD的面积为：$\frac{（2+4）•2}{2}=6$；
∴$S（x）=6×\frac{3}{4}=\frac{9}{2}$；
∴S（x）＞S（2）=4；
∴2＜x＜4，令$-\frac{1}{2}（x-4）^{2}+6=\frac{9}{2}$得：$x=4-\sqrt{3}$，或x=4+$\sqrt{3}$（舍去）；
即P距离A4-$\sqrt{3}$处．

点评 考查矩形、梯形的面积公式，一次函数图象和二次函数图象的画法，分段函数图象的画法，对于分段函数已知函数值求自变量值时，需判断自变量在哪一段上．