题目内容
若实数a,b均不为零,且x2α=
(x>0),则(xα-2xb)9展开式中的常数项等于
______.
| 1 |
| xb |
根据题意,x2α=
,
则(xα-2xb)9=(xα-2x-2a)9,
其展开式为Tr+1=C9r•(xα)9-r•(-2x-2a)r=(-2)r•C93•(xa)9-3r;
令r=3时,可得其展开式的常数项为(-2)3•(xa)9-3r=-672;
故答案为:-672.
| 1 |
| xb |
则(xα-2xb)9=(xα-2x-2a)9,
其展开式为Tr+1=C9r•(xα)9-r•(-2x-2a)r=(-2)r•C93•(xa)9-3r;
令r=3时,可得其展开式的常数项为(-2)3•(xa)9-3r=-672;
故答案为:-672.

练习册系列答案
相关题目
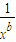 (x>0),则(xα-2xb)9展开式中的常数项等于 .
(x>0),则(xα-2xb)9展开式中的常数项等于 .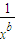 (x>0),则(xα-2xb)9展开式中的常数项等于 .
(x>0),则(xα-2xb)9展开式中的常数项等于 .