题目内容
若实数a,b均不为零,且x2α=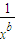 (x>0),则(xα-2xb)9展开式中的常数项等于 .
(x>0),则(xα-2xb)9展开式中的常数项等于 .
【答案】分析:根据题意,x2α= ,代入(xα-2xb)9中可得(xα-2x-2a)9,可得其展开式为Tr+1=(-2)r•C93•(xa)9-3r;进而将r=3代入展开式,计算可得答案.
,代入(xα-2xb)9中可得(xα-2x-2a)9,可得其展开式为Tr+1=(-2)r•C93•(xa)9-3r;进而将r=3代入展开式,计算可得答案.
解答:解:根据题意,x2α=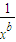 ,
,
则(xα-2xb)9=(xα-2x-2a)9,
其展开式为Tr+1=C9r•(xα)9-r•(-2x-2a)r=(-2)r•C93•(xa)9-3r;
令r=3时,可得其展开式的常数项为(-2)3•(xa)9-3r=-672;
故答案为:-672.
点评:本题考查二项式定理的运用,解题时关键在于对其展开式的形式的记忆与有理数指数幂的化简计算.
 ,代入(xα-2xb)9中可得(xα-2x-2a)9,可得其展开式为Tr+1=(-2)r•C93•(xa)9-3r;进而将r=3代入展开式,计算可得答案.
,代入(xα-2xb)9中可得(xα-2x-2a)9,可得其展开式为Tr+1=(-2)r•C93•(xa)9-3r;进而将r=3代入展开式,计算可得答案.解答:解:根据题意,x2α=
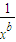 ,
,则(xα-2xb)9=(xα-2x-2a)9,
其展开式为Tr+1=C9r•(xα)9-r•(-2x-2a)r=(-2)r•C93•(xa)9-3r;
令r=3时,可得其展开式的常数项为(-2)3•(xa)9-3r=-672;
故答案为:-672.
点评:本题考查二项式定理的运用,解题时关键在于对其展开式的形式的记忆与有理数指数幂的化简计算.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
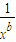 (x>0),则(xα-2xb)9展开式中的常数项等于 .
(x>0),则(xα-2xb)9展开式中的常数项等于 .