题目内容
已知函数f(x)=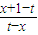 (t为常数).
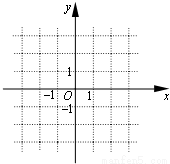
(t为常数).(1)当t=1时,在图中的直角坐标系内作出函数y=f(x)的大致图象,并指出该函数所具备的基本性质中的两个(只需写两个).
(2)设an=f(n)(n∈N*),当t>10,且t∉N*时,试判断数列{an}的单调性并由此写出该数列中最大项和最小项(可用[t]来表示不超过t的最大整数).
(3)利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1)(n≥2,n∈N*),…在上述构造过程中,若xi(i∈N*)在定义域中,则构造数列的过程继续下去;若xi不在定义域中,则构造数列的过程停止.若可用上述方法构造出一个常数列{xn},求t的取值范围.
【答案】分析:(1)当t=1时,f(x)=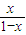 =-1+
=-1+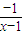 ,画出函数的图象,利用图象可得函数的性质;
,画出函数的图象,利用图象可得函数的性质;
(2)an=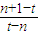 =-1+
=-1+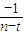 ,确定1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1;n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,由此可得结论
,确定1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1;n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,由此可得结论
(3)只需当x≠t时,方程f(x)=x有解,亦即方程x2+(1-t)x+1-t=0有不等于t的解,由△≥0,可得实数t的取值范围.
解答:解: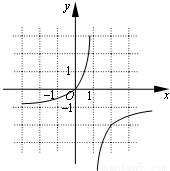 (1)当t=1时,f(x)=
(1)当t=1时,f(x)=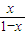 =-1+
=-1+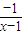 .
.
图象如图(2分)
基本性质:(每个2分)
奇偶性:既非奇函数又非偶函数;
单调性:在(-∞,1)和(1,+∞)上分别递增;
零点:x=0;
最值:无最大、小值.(6分)
(2)an=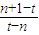 =-1+
=-1+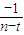 ,
,
当1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1,
当n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,(8分)
因此,数列中的最大项为a[t}=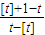 ,(10分)
,(10分)
最小项为a[t}+1=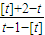 .(12分)
.(12分)
(3)根据题意,只需当x≠t时,方程f(x)=x有解,
亦即方程x2+(1-t)x+1-t=0有不等于t的解,(14分)
将x=t代入方程左边,得左边为1≠0,故方程不可能有x=t的解.(16分)
由△=(1-t)2-4(1-t)≥0,解得t≤-3或t≥1,
即实数t的取值范围是(-∞,-3]∪[1,+∞).(18分)
点评:本题考查函数的图象与性质,考查函数的单调性,考查数列与函数的关系,考查方程解的研究,确定函数的单调性是关键.
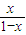 =-1+
=-1+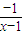 ,画出函数的图象,利用图象可得函数的性质;
,画出函数的图象,利用图象可得函数的性质;(2)an=
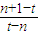 =-1+
=-1+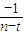 ,确定1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1;n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,由此可得结论
,确定1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1;n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,由此可得结论(3)只需当x≠t时,方程f(x)=x有解,亦即方程x2+(1-t)x+1-t=0有不等于t的解,由△≥0,可得实数t的取值范围.
解答:解:
 (1)当t=1时,f(x)=
(1)当t=1时,f(x)=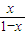 =-1+
=-1+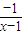 .
.图象如图(2分)
基本性质:(每个2分)
奇偶性:既非奇函数又非偶函数;
单调性:在(-∞,1)和(1,+∞)上分别递增;
零点:x=0;
最值:无最大、小值.(6分)
(2)an=
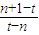 =-1+
=-1+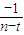 ,
,当1≤n≤[t],n∈N*时,数列单调递增,且此时an均大于-1,
当n≥[t]+1,n∈N*时,数列单调递增,且此时an均小于-1,(8分)
因此,数列中的最大项为a[t}=
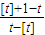 ,(10分)
,(10分)最小项为a[t}+1=
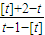 .(12分)
.(12分)(3)根据题意,只需当x≠t时,方程f(x)=x有解,
亦即方程x2+(1-t)x+1-t=0有不等于t的解,(14分)
将x=t代入方程左边,得左边为1≠0,故方程不可能有x=t的解.(16分)
由△=(1-t)2-4(1-t)≥0,解得t≤-3或t≥1,
即实数t的取值范围是(-∞,-3]∪[1,+∞).(18分)
点评:本题考查函数的图象与性质,考查函数的单调性,考查数列与函数的关系,考查方程解的研究,确定函数的单调性是关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|