题目内容
已知函数f(x)=sin(2x+ ),其中
),其中 为实数,若f(x)≤|f(
为实数,若f(x)≤|f( )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( )>f(
)>f( ),则f(x)的单调递增区间是( )
),则f(x)的单调递增区间是( )
 ),其中
),其中 为实数,若f(x)≤|f(
为实数,若f(x)≤|f( )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( )>f(
)>f( ),则f(x)的单调递增区间是( )
),则f(x)的单调递增区间是( )A.[ - - , , + + ](k∈Z) ](k∈Z) |
B.[ , , + + ](k∈Z) ](k∈Z) |
C.[ + + , , + + ](k∈Z) ](k∈Z) |
D.[ - - , , ](k∈Z) ](k∈Z) |
C
由函数解析式知,函数的周期为 .
.
又f(x)≤|f( )|对x∈R恒成立,所以函数的对称轴为x=
)|对x∈R恒成立,所以函数的对称轴为x= +
+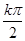 (k∈Z).
(k∈Z).
因此函数的单调区间是[ +
+ ,
, +
+ ]与[
]与[ +
+ ,
,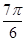 +
+ ](k∈Z).
](k∈Z).
因为函数的对称轴为x= +
+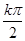 (k∈Z),所以x=
(k∈Z),所以x= +
+ =
= 为一条对称轴,
为一条对称轴,
即f( )=f(
)=f(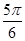 )>f(
)>f( ),而
),而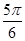 ,
, ∈[
∈[ +
+ ,
,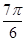 +
+ ],所以[
],所以[ +
+ ,
,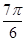 +
+ ]是函数的单调递减区间,即[
]是函数的单调递减区间,即[ +
+ ,
, +
+ ]是f(x)的单调递增区间.
]是f(x)的单调递增区间.
 .
.又f(x)≤|f(
 )|对x∈R恒成立,所以函数的对称轴为x=
)|对x∈R恒成立,所以函数的对称轴为x= +
+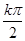 (k∈Z).
(k∈Z).因此函数的单调区间是[
 +
+ ,
, +
+ ]与[
]与[ +
+ ,
,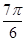 +
+ ](k∈Z).
](k∈Z).因为函数的对称轴为x=
 +
+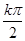 (k∈Z),所以x=
(k∈Z),所以x= +
+ =
= 为一条对称轴,
为一条对称轴,即f(
 )=f(
)=f(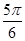 )>f(
)>f( ),而
),而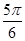 ,
, ∈[
∈[ +
+ ,
,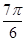 +
+ ],所以[
],所以[ +
+ ,
,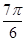 +
+ ]是函数的单调递减区间,即[
]是函数的单调递减区间,即[ +
+ ,
, +
+ ]是f(x)的单调递增区间.
]是f(x)的单调递增区间.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 .
. 的定义域及最小正周期;
的定义域及最小正周期;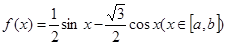 的值域为
的值域为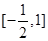 ,设
,设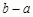 的最大值为
的最大值为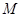 ,最小值为
,最小值为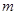 ,则
,则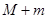 =_________.
=_________. 一个周期的图象(如图),则这个函数的一个解析式为( )
一个周期的图象(如图),则这个函数的一个解析式为( )




 x+
x+ )(x∈R)在区间[-
)(x∈R)在区间[- ,
, ]上的图象,为了得到这个函数图象,只要将y=sinx(x∈R)的图象上所有点( )
]上的图象,为了得到这个函数图象,只要将y=sinx(x∈R)的图象上所有点( )
 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变
倍,纵坐标不变 的图像经过下列平移,可以得到偶函数图像的是( )
的图像经过下列平移,可以得到偶函数图像的是( ) 个单位
个单位 个单位
个单位 cos
cos 的最小正周期为________.
的最小正周期为________. 的部分图象如图所示,则
的部分图象如图所示,则 的值分别是
的值分别是



 的最小正周期是__________________.
的最小正周期是__________________.