题目内容
已知点M(－3,0)、N(3,0)、B(1,0)，动圆C与直线MN切于点B，分别过点M、N且与圆C相切的两条直线相交于点P，则点P的轨迹方程为( )
A．x2－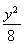
＝1 (x＞1) B．x2－
＝1(x＞0)
C．x2－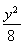
＝1(x＞0) D．x2－
＝1(x＞1)
A
【解析】如图，
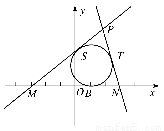
设两切线分别与圆切于点S、T，则|PM|－|PN|＝(|PS|＋|SM|)－(|PT|＋|TN|)＝|SM|－|TN|＝|BM|－|BN|＝2＝2a，所以所求曲线为双曲线的右支且不能与x轴相交，a＝1，c＝3，所以b2＝8，故点P的轨迹方程为x2－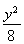
＝1(x＞1)．
练习册系列答案
相关题目
