题目内容
已知函数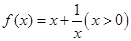 ,以点
,以点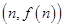 为切点作函数图像的切线
为切点作函数图像的切线 ,直线
,直线 与函数
与函数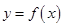 图像及切线
图像及切线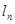 分别相交于
分别相交于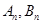 ,记
,记 .
.
(1)求切线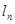 的方程及数列
的方程及数列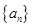 的通项;
的通项;
(2)设数列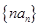 的前
的前 项和为
项和为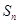 ,求证:
,求证: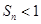 .
.
(1)切线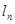 的方程为
的方程为 ,数列
,数列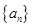 的通项公式为
的通项公式为 ;(2)详见试题解析.
;(2)详见试题解析.
解析试题分析:(1)由导数的几何意义,先对函数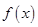 求导,求导函数
求导,求导函数 在
在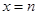 处的函数值,即得切线的斜率,最后由直线的点斜式方程即可求得切线
处的函数值,即得切线的斜率,最后由直线的点斜式方程即可求得切线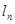 的方程,进一步结合已知条件可得
的方程,进一步结合已知条件可得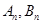 的坐标,由两点间的距离公式可得数列
的坐标,由两点间的距离公式可得数列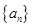 的通项;(2)首先写出数列
的通项;(2)首先写出数列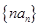 的前
的前 项和
项和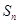 的表达式,根据数列
的表达式,根据数列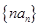 通项公式的结构特征选择裂项相消法求和
通项公式的结构特征选择裂项相消法求和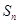 ,进而可证明不等式
,进而可证明不等式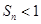 .
.
试题解析:(1)对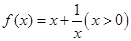 求导,得
求导,得 ,则切线
,则切线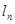 方程为:
方程为: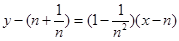 ,即
,即 ,易知
,易知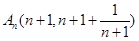 ,
,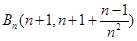 ,
,
由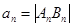 知
知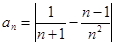 =
= .
.
(2)
 =
=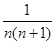 =
=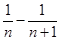 ,
,
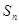 =
=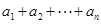 =
= =
=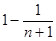 <1.
<1.
考点:1.导数的几何意义;2.数列通项公式及前 项和的求法(裂项相消法);3.数列不等式的证明.
项和的求法(裂项相消法);3.数列不等式的证明.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
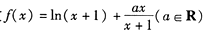
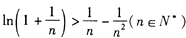
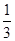 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c. ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.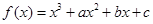 在
在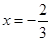 与
与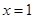 时都取得极值.
时都取得极值.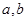 的值及
的值及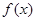 的极大值与极小值;
的极大值与极小值;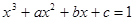 有三个互异的实根,求
有三个互异的实根,求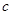 的取值范围;
的取值范围;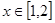 ,不等式
,不等式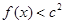 恒成立,求
恒成立,求 ,
, ,
,
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; ,都有
,都有 恒成立,求
恒成立,求 的最小值;
的最小值; ,
, ,若
,若 ,
, 为曲线
为曲线 的两个不同点,满足
的两个不同点,满足 ,且
,且 ,使得曲线
,使得曲线 在
在 处的切线与直线AB平行,求证:
处的切线与直线AB平行,求证: