题目内容
已知椭圆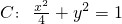 的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.
的右焦点为F,右准线为l,过F作直线交椭圆C于点P、Q两点.
(I)设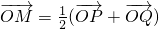 (O为坐标原点),求M的轨迹方程;
(O为坐标原点),求M的轨迹方程;
(II)设N是l上的任一点,求证:∠PNQ<90°.
解:(1)设M(x,y),P(x1,y1),Q(x2,y2),由题设知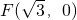 .由
.由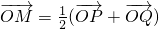 ,知M为PQ之中点,∴
,知M为PQ之中点,∴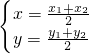 又P、Q在椭圆C上,则
又P、Q在椭圆C上,则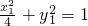 ,
,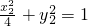 .当x1≠x2时,两式相减,得
.当x1≠x2时,两式相减,得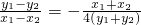 ,即
,即 ,又
,又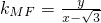 ,所以
,所以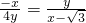 ,化简得
,化简得 .
.
当x1=x2时,即PQ垂直于x轴时,此时M的坐标为(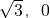 ),也是满足上式.故所求的轨迹方程为
),也是满足上式.故所求的轨迹方程为 .
.
(II)过P、Q及PQ之中点R,分别作右准线l的垂线PP1,QQ1,RR1,垂足为P1,Q,R1,由椭圆的定义,知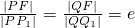 ,∴
,∴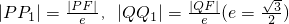 .
.
又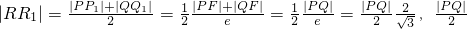 ,
,
所以以PQ为直径的圆与l相离,所以N在以PQ为直径的圆外,所以∠PNQ<90°.
分析:(1)设M(x,y),P(x1,y1),Q(x2,y2),由题设知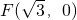 .由
.由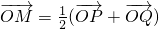 ,知M为PQ之中点,知
,知M为PQ之中点,知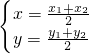 ,由P、Q在椭圆C上,有
,由P、Q在椭圆C上,有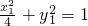 ,
,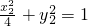 .由点差法能够得到所求的轨迹方程.
.由点差法能够得到所求的轨迹方程.
(II)过P、Q及PQ之中点R,分别作右准线l的垂线PP1,QQ1,RR1,垂足为P1,Q,R1,由椭圆的定义,知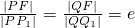 ,故
,故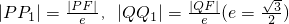 .由此能够证明∠PNQ<90°.
.由此能够证明∠PNQ<90°.
点评:本题考查M的轨迹方程的求法和证明∠PNQ<90°.解题时要认真审题,注意合理地进行等价转化.
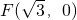 .由
.由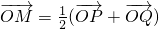 ,知M为PQ之中点,∴
,知M为PQ之中点,∴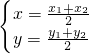 又P、Q在椭圆C上,则
又P、Q在椭圆C上,则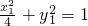 ,
,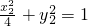 .当x1≠x2时,两式相减,得
.当x1≠x2时,两式相减,得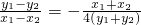 ,即
,即 ,又
,又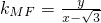 ,所以
,所以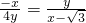 ,化简得
,化简得 .
.当x1=x2时,即PQ垂直于x轴时,此时M的坐标为(
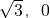 ),也是满足上式.故所求的轨迹方程为
),也是满足上式.故所求的轨迹方程为 .
.(II)过P、Q及PQ之中点R,分别作右准线l的垂线PP1,QQ1,RR1,垂足为P1,Q,R1,由椭圆的定义,知
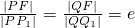 ,∴
,∴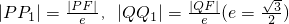 .
.又
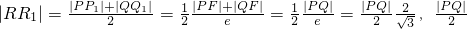 ,
,所以以PQ为直径的圆与l相离,所以N在以PQ为直径的圆外,所以∠PNQ<90°.
分析:(1)设M(x,y),P(x1,y1),Q(x2,y2),由题设知
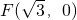 .由
.由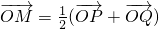 ,知M为PQ之中点,知
,知M为PQ之中点,知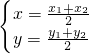 ,由P、Q在椭圆C上,有
,由P、Q在椭圆C上,有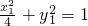 ,
,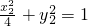 .由点差法能够得到所求的轨迹方程.
.由点差法能够得到所求的轨迹方程.(II)过P、Q及PQ之中点R,分别作右准线l的垂线PP1,QQ1,RR1,垂足为P1,Q,R1,由椭圆的定义,知
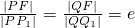 ,故
,故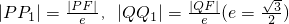 .由此能够证明∠PNQ<90°.
.由此能够证明∠PNQ<90°.点评:本题考查M的轨迹方程的求法和证明∠PNQ<90°.解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C