题目内容
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
),点D对跑道AB的视角为 .
.

(1)将tan 表示为x的函数:
表示为x的函数:
(2)求点D的位置,使得 取得最大值.
取得最大值.
 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
),点D对跑道AB的视角为 .
.
(1)将tan
 表示为x的函数:
表示为x的函数:(2)求点D的位置,使得
 取得最大值.
取得最大值.(1)
(2)当 时,
时, 取得最大值,即
取得最大值,即 取得最大值
取得最大值

(2)当
 时,
时, 取得最大值,即
取得最大值,即 取得最大值
取得最大值试题分析:解:(Ⅰ)过A分别作直线CD、BC的垂线,垂足分别为E,F.

由题设知,∠ABF=30°,∴
 ,
,又
 ,∵
,∵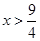 时,
时,
∴

 ,其中
,其中
即
 7分
7分(Ⅱ)记
 ,由
,由 可知
可知 是锐角.
是锐角.而
 10分
10分∴
 在区间
在区间 上单调递增,
上单调递增,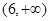 上单调递减,
上单调递减,函数
 在
在 时取得最大值
时取得最大值 ,
, 而
 上是增函数,所以当
上是增函数,所以当 时,
时, 取得最大值,即
取得最大值,即 取得最大值.
取得最大值.答:在海岸线l上距离C点6km处的D点观看飞机跑道的视角最大. 13分
点评:主要是考查了导数在援救函数中的运用,求解最值,属于中档题。

练习册系列答案
相关题目
 ,
, .
. 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
,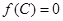 且
且 ,求
,求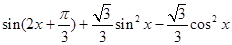 .
.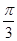 个单位长度,得到函数g(x)的图象,求g (x)在区间
个单位长度,得到函数g(x)的图象,求g (x)在区间 上的值域.
上的值域.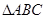 中,角
中,角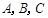 所对的边分别为
所对的边分别为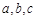 ,且满足
,且满足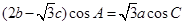 .
. 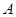 的大小;
的大小; 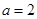 ;②
;②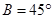 ;③
;③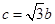 .试从中选出两个可以确定
.试从中选出两个可以确定 的结果是( )
的结果是( )



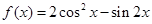
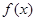 的最小正周期和值域;
的最小正周期和值域;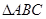 的内角
的内角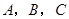 所对的边分别为
所对的边分别为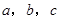 ,若
,若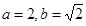 ,且
,且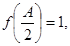 求
求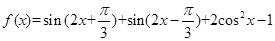 ,
,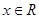 .
.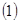 求函数
求函数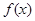 的最小正周期;
的最小正周期;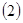 若函数
若函数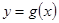 的图像和
的图像和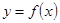 的图像关于直线
的图像关于直线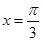 对称,求
对称,求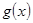 在
在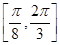 上的最大值和最小值.
上的最大值和最小值.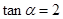 ,则
,则 _______.
_______.