题目内容
已知双曲线中心在原点,焦点在x轴上,实轴长为2.一条斜率为1的直线经过双曲线的右焦点与双曲线相交于A、B两点,以AB为直径的圆与双曲线的右准线相交于M、N.(1)若双曲线的离心率2,求圆的半径;
(2)设AB中点为H,若
 ,求双曲线方程.
,求双曲线方程.
【答案】分析:(1)设出双曲线方程,将直线方程代入,求出半径即可.
(2)设出双曲线方程,直线方程代入化简为一元二次方程,并根据韦达定理化简,最后求出c
解答:解:(1)设双曲线方程为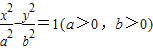
由题知: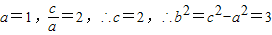
∴双曲线方程为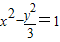 右焦点F(2,0)
右焦点F(2,0)
故直线l的方程为y=x-2代入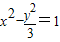 中得:2x2+4x-7=0
中得:2x2+4x-7=0
设A(x1,y1),B(x2,y2),则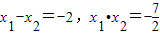
∴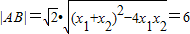
∴半径r=3
(2)设双曲线方程为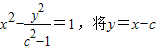 代入并整理得(c2-2)x2+2cx-2c2+1=0,
代入并整理得(c2-2)x2+2cx-2c2+1=0,
由韦达定理: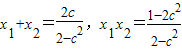
设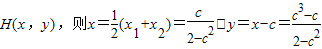
设圆半径为R且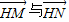 的夹角为θ,
的夹角为θ,
则
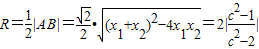
∴
∴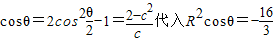 中
中
得:c2=3,
∴所求的双曲线方程为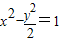 .
.
点评:本题考查圆锥曲线综合运用,以及双曲线的标准方程,平面向量的数量级运算,通过对多种知识的综合理解,考查对知识的综合运用能力,属于中档题.
(2)设出双曲线方程,直线方程代入化简为一元二次方程,并根据韦达定理化简,最后求出c
解答:解:(1)设双曲线方程为
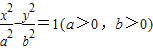
由题知:
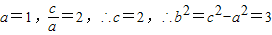
∴双曲线方程为
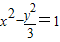 右焦点F(2,0)
右焦点F(2,0)故直线l的方程为y=x-2代入
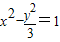 中得:2x2+4x-7=0
中得:2x2+4x-7=0设A(x1,y1),B(x2,y2),则
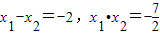
∴
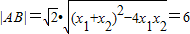
∴半径r=3
(2)设双曲线方程为
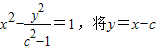 代入并整理得(c2-2)x2+2cx-2c2+1=0,
代入并整理得(c2-2)x2+2cx-2c2+1=0,由韦达定理:
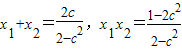
设
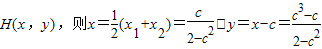
设圆半径为R且
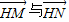 的夹角为θ,
的夹角为θ,则

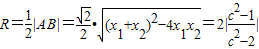
∴

∴
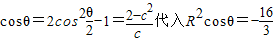 中
中得:c2=3,
∴所求的双曲线方程为
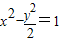 .
.点评:本题考查圆锥曲线综合运用,以及双曲线的标准方程,平面向量的数量级运算,通过对多种知识的综合理解,考查对知识的综合运用能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知双曲线中心在原点且一个焦点为F(
,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为-
,则此双曲线的方程是( )
| 7 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线中心在原点且一个焦点为F1(-
, 0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程为( )
| 5 |
A、
| ||||
B、x2-
| ||||
C、
| ||||
D、
|