题目内容
不等式组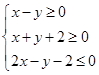 所确定的平面区域记为
所确定的平面区域记为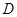 ,则
,则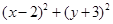 的最大值为
的最大值为
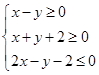 所确定的平面区域记为
所确定的平面区域记为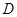 ,则
,则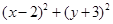 的最大值为
的最大值为 | A.13 | B.25 | C.5 | D.16 |
B
分析:根据约束条件画出可行域,对于可行域不要求线性目标函数的最值,而是求可行域D内的点与点(2,-3)的距离的最大值,保证圆在区域D内,然后求出(x-2)2+(y+3)2的最大值.
解:画出不等式组
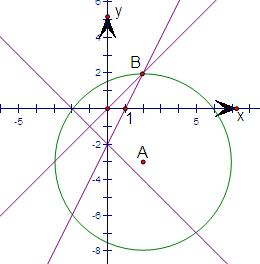
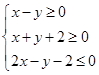 不等式组所表示的平面区域,如图圆,
不等式组所表示的平面区域,如图圆,其中离点(2,-3)最远的点为B(2,2),距离为:5,
则(x-2)2+(y+3)2的最大值为:25.
故选B,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
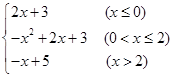 的最大值是 ( )
的最大值是 ( )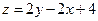 ,式中
,式中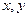 满足条件
满足条件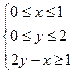 ,求
,求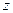 的最大值和最小值。
的最大值和最小值。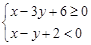 表示的平面区域是( )
表示的平面区域是( )
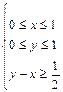 下,z = 4-2x+y的最大值是 .
下,z = 4-2x+y的最大值是 .
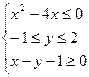 表示的平面区域为M,
表示的平面区域为M,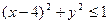 表示的平面区域为N,现随机向区域M内抛一点,则该点落在平面区域N内的概率是
表示的平面区域为N,现随机向区域M内抛一点,则该点落在平面区域N内的概率是 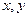 满足约束条件:
满足约束条件: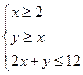 ,则
,则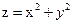 的最大值为
的最大值为 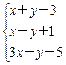 设y=kx,则k的取值范围是( ).
设y=kx,则k的取值范围是( ).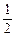 ,
,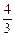 ]
]