题目内容
已知等差数列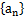 满足:
满足: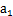 =2,且
=2,且 成等比数列.
成等比数列.
(1)求数列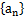 的通项公式.
的通项公式.
(2)记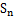 为数列
为数列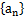 的前n项和,是否存在正整数n,使得
的前n项和,是否存在正整数n,使得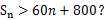 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由.
(1)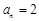 或
或 ;(2)当
;(2)当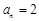 时,不存在满足题意的n;当
时,不存在满足题意的n;当 时,存在满足题意的n,其最小值为41.
时,存在满足题意的n,其最小值为41.
解析试题分析:(1)本小题利用基本量法,设公差为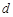 ,则
,则 成等比可转化为关于
成等比可转化为关于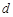 的方程,解出
的方程,解出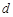 即可写其通项公式;(2)在上小题已得的等差数列的前提下,求出其前n项和,利用
即可写其通项公式;(2)在上小题已得的等差数列的前提下,求出其前n项和,利用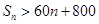 转化为不等解集问题的分析即可,同时要注意n为正整数.
转化为不等解集问题的分析即可,同时要注意n为正整数.
试题解析:(1)设数列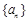 的公差为
的公差为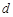 ,依题意,
,依题意,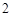 ,
,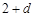 ,
,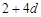 成等比数列,故有
成等比数列,故有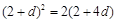 ,
,
化简得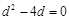 ,解得
,解得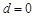 或
或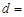
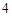 .当
.当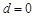 时,
时,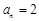 ;当
;当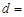
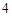 时,
时,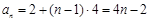 ,
,
从而得数列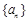 的通项公式为
的通项公式为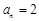 或
或 .
.
(2)当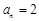 时,
时,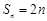 .显然
.显然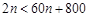 ,此时不存在正整数n,使得
,此时不存在正整数n,使得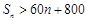 成立.
成立.
当 时,
时,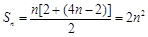 .令
.令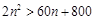 ,即
,即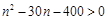 ,解得
,解得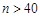 或
或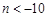 (舍去),此时存在正整数n,使得
(舍去),此时存在正整数n,使得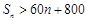 成立,n的最小值为41.
成立,n的最小值为41.
综上,当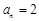 时,不存在满足题意的n;当
时,不存在满足题意的n;当 时,存在满足题意的n,其最小值为41.
时,存在满足题意的n,其最小值为41.
考点:等差与等比数列的定义,通项公式,等差数列的前n项和公式,解一元二次不等式,分类讨论与化归思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
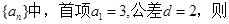
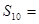
 满足
满足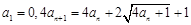 ,令
,令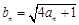 .
. 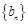 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;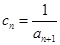 ,求
,求 前
前 项的和
项的和 ;
;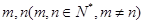 使得
使得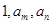 三数成等比数列?
三数成等比数列? 满足:
满足: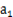 =2,且
=2,且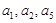 成等比数列.
成等比数列.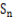 为数列
为数列 若存在,求n的最小值;若不存在,说明理由.
若存在,求n的最小值;若不存在,说明理由. 的前
的前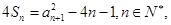 且
且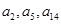 构成等比数列.(1) 证明:
构成等比数列.(1) 证明: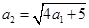 ;(2) 求数列
;(2) 求数列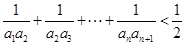 .
.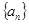 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.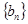 是等差数列;
是等差数列; 的前
的前 项和为
项和为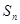 ,
, ,
,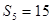 ,
, ,求数列
,求数列 的前100项和.
的前100项和.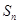 为等差数列
为等差数列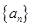 的前
的前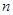 项和,若
项和,若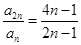 ,则
,则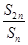 =________;
=________;