��Ŀ����
����ԲC��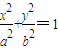 ��a��b��0����һ����������ΪA��
��a��b��0����һ����������ΪA��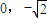 ���������ҽ��㵽ֱ��
���������ҽ��㵽ֱ��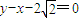 �ľ���Ϊ3��
�ľ���Ϊ3����1������ԲC�Ĺ켣���̣�
��2����A��B����ԲC�ϵIJ�ͬ���㣬��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��
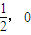 ������֤��M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
������֤��M�����С�����ҡ����е���ͬһ��ֱ���ϣ���3�����ݽ�����⣨2���ľ�������ᣬ��������ȡ��ƹ��˼�뷽�������һ���롰����ҡ��йصľ����о���ֵ�Ľ��ۣ������Խ��������С�⽫�������������IJ���Ը��費ͬ�ķ�ֵ��
���𰸡���������1��������Բ�Ľ�����x���ϣ���֪��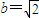 �������ҽ��㵽ֱ��
�������ҽ��㵽ֱ��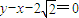 �ľ���Ϊ3���ɵ�
�ľ���Ϊ3���ɵ�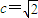 ���Ӷ�����a=2���ʿɵ���ԲC�Ĺ켣���̣�
���Ӷ�����a=2���ʿɵ���ԲC�Ĺ켣���̣�
��2������A��x1��y1����B��x2��y2�����е�ΪP��x��y��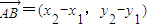 ��
��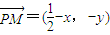
����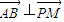 ������
������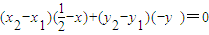 �����õ�����Բ�ϣ��У�x1-x2����x1+x2��+2��y1-y2����y1+y2��=0���ɴ��ܵ�����M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ�
�����õ�����Բ�ϣ��У�x1-x2����x1+x2��+2��y1-y2����y1+y2��=0���ɴ��ܵ�����M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ�
��3����Բ��һ�㣬�㵽һ�㼴�ɵý��ۣ���A��B����Բ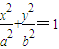 ��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������
��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������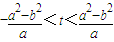 ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
����⣺��1��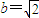 ��
��
�����ҽ��㵽ֱ��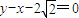 �ľ���Ϊ3���ɵ�
�ľ���Ϊ3���ɵ�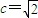 ����a=2
����a=2
����ԲC�ı����̣�
��2����A��x1��y1����B��x2��y2�����е�ΪP��x��y��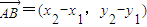 ��
��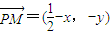
����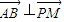 ������
������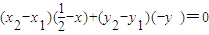 ����
����
��x12+2y12��x22+2y22�ڣ�
�ɢ٢���ʽ����ã�x12-x22+2y12-2y22=0
����x1-x2����x1+x2��+2��y1-y2����y1+y2��=0����
�ɣ������ã�x=1
��ˣ���M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ�
��3����Բ��һ�㣬�㵽һ��
��A��B����Բ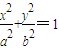 ��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������
��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������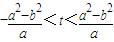 ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
����������Ŀ�����ֱ����Բ���ߵ��ۺ����⣬��Ҫ������Բ�����̵���⣬�������ͬʱ����ѧ��̽����������һ�����Ѷȣ�
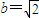 �������ҽ��㵽ֱ��
�������ҽ��㵽ֱ��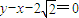 �ľ���Ϊ3���ɵ�
�ľ���Ϊ3���ɵ�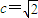 ���Ӷ�����a=2���ʿɵ���ԲC�Ĺ켣���̣�
���Ӷ�����a=2���ʿɵ���ԲC�Ĺ켣���̣���2������A��x1��y1����B��x2��y2�����е�ΪP��x��y��
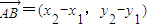 ��
��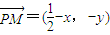
����
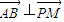 ������
������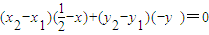 �����õ�����Բ�ϣ��У�x1-x2����x1+x2��+2��y1-y2����y1+y2��=0���ɴ��ܵ�����M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ�
�����õ�����Բ�ϣ��У�x1-x2����x1+x2��+2��y1-y2����y1+y2��=0���ɴ��ܵ�����M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ���3����Բ��һ�㣬�㵽һ�㼴�ɵý��ۣ���A��B����Բ
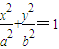 ��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������
��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������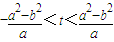 ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�����⣺��1��
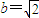 ��
�������ҽ��㵽ֱ��
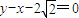 �ľ���Ϊ3���ɵ�
�ľ���Ϊ3���ɵ�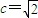 ����a=2
����a=2����ԲC�ı����̣�

��2����A��x1��y1����B��x2��y2�����е�ΪP��x��y��
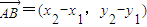 ��
��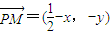
����
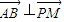 ������
������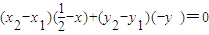 ����
������x12+2y12��x22+2y22�ڣ�
�ɢ٢���ʽ����ã�x12-x22+2y12-2y22=0
����x1-x2����x1+x2��+2��y1-y2����y1+y2��=0����
�ɣ������ã�x=1
��ˣ���M�����С�����ҡ����е���ͬһ��ֱ��x=1�ϣ�
��3����Բ��һ�㣬�㵽һ��
��A��B����Բ
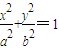 ��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������
��a��b��0�����ϵIJ�ͬ���㣮��AB����ƽ����y�ᣩ�Ĵ�ֱƽ������x���ཻ�ڵ�M�������AB�ǵ�M��һ��������ҡ��������M������ΪM��t��0������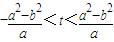 ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
ʱ��֤������M�����С�����ҡ����е���ͬһ��ֱ���ϣ�����������Ŀ�����ֱ����Բ���ߵ��ۺ����⣬��Ҫ������Բ�����̵���⣬�������ͬʱ����ѧ��̽����������һ�����Ѷȣ�

��ϰ��ϵ�д�
�����Ŀ
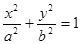 ��a>b>0�������ҽ���ֱ�ΪF1��F2��P��C�ϵĵ㣬
��a>b>0�������ҽ���ֱ�ΪF1��F2��P��C�ϵĵ㣬 ��
��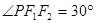 ����C��������Ϊ( )
����C��������Ϊ( )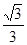 B��
B��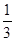 C��
C�� D��
D��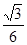
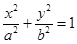 ��a>b>0�����㣨0,4����������Ϊ
��a>b>0�����㣨0,4����������Ϊ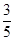
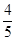 ��ֱ�߱���ԲC�����߶ε��е����ꡣ
��ֱ�߱���ԲC�����߶ε��е����ꡣ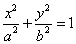 ��a��b��0�����㣨0��4����������Ϊ
��a��b��0�����㣨0��4����������Ϊ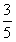 ��
��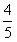 ��ֱ�߱�C�����߶ε��е����ꡣ
��ֱ�߱�C�����߶ε��е����ꡣ ��a��b��0�� �����ҽ���ֱ�ΪF1��F2���϶���ΪA������A��AF2��ֱ��ֱ�߽�x�Ḻ�����ڵ�Q����
��a��b��0�� �����ҽ���ֱ�ΪF1��F2���϶���ΪA������A��AF2��ֱ��ֱ�߽�x�Ḻ�����ڵ�Q���� ��
��  ���У�����ԲC�ķ��̣�
���У�����ԲC�ķ��̣� 
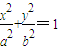 ��a��b��0����һ����������ΪA��
��a��b��0����һ����������ΪA��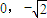 ���������ҽ��㵽ֱ��
���������ҽ��㵽ֱ��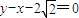 �ľ���Ϊ3��
�ľ���Ϊ3��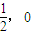 ������֤����M�����С�����ҡ����е���ͬһ��ֱ���ϣ�
������֤����M�����С�����ҡ����е���ͬһ��ֱ���ϣ�