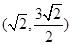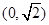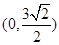题目内容
点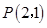 为圆
为圆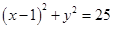 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B.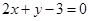 | C.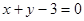 | D.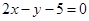 |
C
解析试题分析:由弦中点与圆心连线垂直于弦所在直线得:弦所在直线斜率为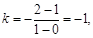 再由点斜式得直线
再由点斜式得直线 的方程为
的方程为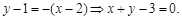 善于利用几何条件揭示特征值(直线斜率)是解析几何一个基本思想方法.
善于利用几何条件揭示特征值(直线斜率)是解析几何一个基本思想方法.
考点:直线与圆关系(弦中点与圆心连线垂直于弦所在直线),点斜式直线方程.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知圆的方程为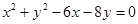 .设该圆过点
.设该圆过点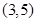 的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A.10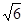 | B.20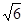 | C.30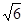 | D.40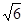 |
已知圆 ,圆
,圆 与圆
与圆 关于直线
关于直线 对称,则圆
对称,则圆 的方程为( )
的方程为( )
A. | B. |
C. | D. |
圆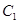 :
: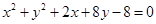 与圆
与圆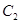 :
: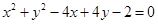 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
直线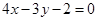 与圆
与圆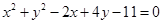 的位置关系是( )
的位置关系是( )
| A.相离 | B.相切 | C.相交过圆心 | D.相交不过圆心 |
在平面直角坐标系内,若圆 :
: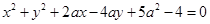 的圆心在第二象限内,则实数
的圆心在第二象限内,则实数 的取值范围为( )
的取值范围为( )
A.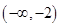 | B.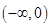 | C.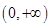 | D.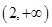 |
直线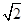 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
| A.0 | B.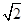 | C.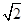 -1 -1 | D.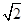 +1 +1 |
当直线l:y=k(x-1)+2被圆C:(x-2)2+(y-1)2=5截得的弦最短时,k的值为 ( ).
| A.2 | B.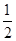 | C.3 | D.1 |
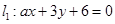 ,
,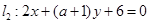 ,和圆C:
,和圆C: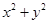
 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )