题目内容
在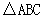 中,内角A,B,C所对的分别是a,b,c。已知a=2,c=
中,内角A,B,C所对的分别是a,b,c。已知a=2,c=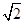 ,cosA=
,cosA= .
.
(I)求sinC和b的值;
(II)求 的值。
的值。
【考点定位】本小题主要考查同角三角函数的基本关系、二倍角的正弦与余弦公式、两角和余弦公式以及正弦定理、余弦定理等基础知识,考查基本运算求解能力.
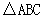 中,内角A,B,C所对的分别是a,b,c。已知a=2,c=
中,内角A,B,C所对的分别是a,b,c。已知a=2,c=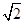 ,cosA=
,cosA= .
.(I)求sinC和b的值;
(II)求
 的值。
的值。【考点定位】本小题主要考查同角三角函数的基本关系、二倍角的正弦与余弦公式、两角和余弦公式以及正弦定理、余弦定理等基础知识,考查基本运算求解能力.
(I)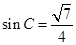 ,b=1 (2)
,b=1 (2) 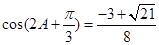
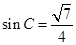 ,b=1 (2)
,b=1 (2) 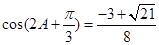
(I)解:在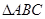 中,由
中,由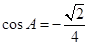 ,可得
,可得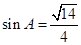 .又由
.又由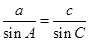 及a=2,
及a=2,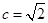 ,可得
,可得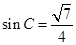 .
.
由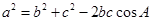 ,得
,得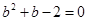 .因为
.因为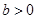 ,故解得b=1.
,故解得b=1.
所以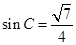 ,b=1.
,b=1.
(II)解:由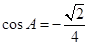 ,
,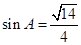 ,得
,得 .
.
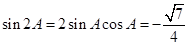
所以,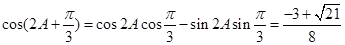
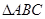 中,由
中,由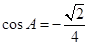 ,可得
,可得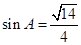 .又由
.又由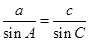 及a=2,
及a=2,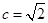 ,可得
,可得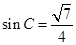 .
.由
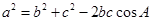 ,得
,得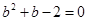 .因为
.因为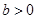 ,故解得b=1.
,故解得b=1.所以
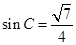 ,b=1.
,b=1.(II)解:由
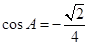 ,
,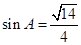 ,得
,得 .
.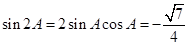
所以,
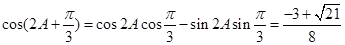

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象向右平移
的图象向右平移 个单位, 再将所得图象上各点横坐标伸长到原来的3倍(纵坐标不变), 再将所得图象上各点纵坐标伸长为原来的4倍(横坐标不变), 得到函数
个单位, 再将所得图象上各点横坐标伸长到原来的3倍(纵坐标不变), 再将所得图象上各点纵坐标伸长为原来的4倍(横坐标不变), 得到函数 的图象;
的图象;
 (
( )的最小正周期是
)的最小正周期是 ,若其图像向右平移
,若其图像向右平移 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数 的图像
的图像 对称
对称 对称
对称 对称
对称 对称
对称
 的图象与x轴交点为
的图象与x轴交点为 ,相邻最高点坐标为
,相邻最高点坐标为 .
.  的表达式;
的表达式; 的单调增区间;
的单调增区间; 在
在 上的最值.
上的最值. 的周期,振幅,初相分别是( )
的周期,振幅,初相分别是( )



 且在
且在 上的最大值为
上的最大值为 ,
,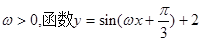 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值是( )
的最小值是( )


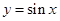 为增函数的是
为增函数的是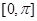
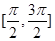
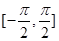
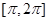
 为锐角,且cos
为锐角,且cos
 ,cos
,cos
 ,则
,则 的值是_____________.
的值是_____________.